Даны два числа \(a\) и \(b\). Выведите гипотенузу треугольника с заданными катетами.
| Ввод | Вывод |
|---|---|
3 |
5.0 |
\(n\) школьников делят \(k\) яблок поровну, неделяющийся остаток остается в корзинке. Сколько яблок достанется каждому школьнику? Сколько яблок останется в корзинке? Программа получает на вход числа \(n\) и \(k\) и должна вывести два числа: количество яблок у каждого школьника и количество яблок, оставшихся в корзинке.
| Ввод | Вывод |
|---|---|
3 |
4 2 |
Феофилакт хочет купить ракетки и шарики для игры в настольный теннис. Один комплект ракеток стоит \(a\) рублей, один шарик стоит \(b\) рублей. У Феофилакта есть \(c\) рублей, \(c\ge a\), он покупает один комплект ракеток и шарики на оставшиеся деньги. Сколько шариков купит Феофилакт?
Программа получает на вход три числа: \(a\), \(b\), \(c\).
| Ввод | Вывод |
|---|---|
20 |
3 |
Дано двузначное число. Определите его первую цифру (количество десятков) и последнюю цифру (количество единиц).
| Ввод | Вывод |
|---|---|
42 |
4 |
Дано натуральное число, не меньшее 10. Найдите число десятков в его десятичной записи (то есть предпоследнюю цифру его десятичной записи).
| Ввод | Вывод |
|---|---|
179 |
7 |
Дано трехзначное число. Найдите сумму его цифр.
| Ввод | Вывод |
|---|---|
179 |
17 |
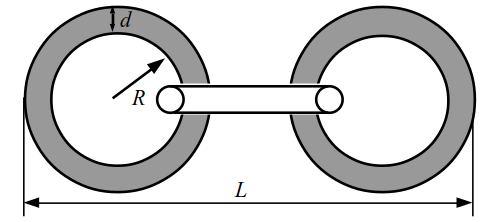
Из проволоки толщиной \(d\) миллиметров сделали кольца. Внутренний радиус каждого кольца составляет \(R\) миллиметров. Всего сделали \(n\) колец и их соединили в цепь. Определите длину получившейся цепи \(L\). На рисунке изображен пример для \(n = 3\).

Программа получает на вход числа \(d\), \(R\), \(n\), при этом \(d\lt R\), и должна вывести длину полученной цепи.
| Ввод | Вывод |
|---|---|
2 |
64 |
С начала суток прошло \(n\) минут. Определите, сколько часов и минут будут показывать электронные часы в этот момент. Программа должна вывести два числа: количество часов (от 0 до 23) и количество минут (от 0 до 59).
| Ввод | Вывод |
|---|---|
150 |
2 30 |
Пирожок в столовой стоит \(a\) рублей и \(b\) копеек. Определите, сколько рублей и копеек нужно заплатить за \(n\) пирожков. Программа получает на вход три числа: \(a\), \(b\), \(n\), и должна вывести два числа: стоимость покупки в рублях и копейках.
| Ввод | Вывод |
|---|---|
10 |
20 30 |
2 |
10 0 |
Длина Московской кольцевой автомобильной дороги —109 километров. Байкер Вася стартует с нулевого километра МКАД и едет со скоростью \(v\) километров в час. На какой отметке он остановится через \(t\) часов?
Программа получает на вход значение \(v\) и \(t\). Если \(v>0\), то Вася движется в положительном направлении по МКАД, если же значение \(v\lt 0\), то в отрицательном.
Программа должна вывести целое число от 0 до 108 — номер отметки, на которой остановится Вася.
| Ввод | Вывод |
|---|---|
60 |
11 |
-1 |
108 |
Дано целое число \(n\). Выведите следующее за ним четное число.
| Ввод | Вывод |
|---|---|
7 |
8 |
8 |
10 |
Шахматная доска состоит из \(n \times m\) клеток, покрашенных в черный и белый цвет в шахматном порядке. При этом клетка в левом нижнем углу доски покрашена в черный цвет. Определите, сколько всего на доске черных клеток.
Программа получает на вход числа \(n\) и \(m\).
| Ввод | Вывод |
|---|---|
3 |
6 |
В некоторой школе решили набрать три новых математических класса и оборудовать кабинеты для них новыми партами. За каждой партой может сидеть двое учащихся. Известно количество учащихся в каждом из трех классов. Выведите наименьшее число парт, которое нужно приобрести для них.
Программа получает на вход три натуральных числа: количество учащихся в каждом из трех классов.
| Ввод | Вывод |
|---|---|
25 |
40 |
Напишите программу, которая считывает значения двух переменных \(a\) и \(b\), затем меняет их значения местами и выводит их значения на экран.
Вам нужно модифицировать пример ниже, добавив на место многоточия несколько строчек. Модифицировать ввод-вывод в этом примере нельзя.
a = int(input()) b = int(input()) ... ... print(a, b)
| Ввод | Вывод |
|---|---|
3 |
7 3 |
Примечание для знающих Питон — забудьте про существование кортежей. Используйте вспомогательную переменную.
Решите предыдущую задачу без использования вспомогательной переменной (ну и без кортежных присваиваний, разумеется).
Ручка стоила \(K\) рублей. Первого сентября стоимость ручки увеличилась ровно на \(P\) процентов. Определите, сколько ручек можно купить на \(S\) рублей после подорожания.
Программа получает на вход три числа: \(K\), \(P\), \(S\).
| Ввод | Вывод |
|---|---|
33 |
2 |
Пояснение к примеру. После подорожания ручка стала стоить 34 рубля 65 копеек. На 100 рублей можно купить 2 ручки.
В некоторой школе занятия начинаются в 9:00. Продолжительность урока — 45 минут, после 1-го, 3-го, 5-го и т.д. уроков перемена 5 минут, а после 2-го, 4-го, 6-го и т.д. — 15 минут.
Дан номер урока (число от 1 до 10). Определите, когда заканчивается указанный урок. Выведите два целых числа: время окончания урока в часах и минутах.
| Ввод | Вывод |
|---|---|
3 |
11 35 |
2 |
10 35 |
На каждой странице книги напечатано ровно \(k\) строк: на первой странице находятся строки с \(1\) по \(k\), на второй — c \(k+1\) по \(2k\) и т.д. Определите, на какой странице находится строка номер \(n\) и какой по счёту будет эта строка на странице.
Даны числа \(k\) и \(n\), нужно вывести два числа: номер страницы и номер строки на странице.
| Ввод | Вывод |
|---|---|
50 |
2 50 |
За день машина проезжает \(n\) километров. Сколько дней нужно, чтобы проехать маршут длиной \(m\) километров?
Программа получает на вход числа \(n\) и \(m\).
| Ввод | Вывод |
|---|---|
700 |
2 |
700 |
3 |
\(n\) школьников делят \(k\) яблок “поровну”, то есть так, чтобы количество яблок, доставшихся любым двум школьникам, отличалось бы не более, чем на 1.
Программа получает на вход числа \(n\) и \(k\) и должна вывести количество школьников, которым достанется яблок меньше, чем некоторым из их товарищей.
| Ввод | Вывод |
|---|---|
7 |
5 |
7 |
0 |
Улитка ползет по вертикальному шесту высотой \(h\) метров, поднимаясь за день на \(a\) метров, а за ночь спускаясь на \(b\) метров. На какой день улитка доползет до вершины шеста?
Программа получает на вход натуральные числа \(h\), \(a\), \(b\), и должна вывести одно натуральное число. Гарантируется, что \(h\ge a\gt b\).
| Ввод | Вывод |
|---|---|
10 |
8 |
Электронные часы показывают время в формате h:mm:ss, то есть сначала записывается
количество часов, потом обязательно двузначное количество минут, затем обязательно двузначное количество секунд.
Количество минут и секунд при необходимости дополняются до двузначного числа нулями.
С начала суток прошло \(n\) секунд. Выведите, что покажут часы. Обратите внимание, что \(n\) может быть больше количества секунд в сутках.
| Ввод | Вывод |
|---|---|
3602 |
1:00:02 |
129700 |
12:01:40 |
В часах села батарейка, и они стали идти вдвое медленнее. Когда на часах было \(x_1\) часов \(y_1\) минут, правильное время было \(a_1\) часов \(b_1\) минут. Сколько времени будет на самом деле, когда часы в следующий раз покажут \(x_2\) часов \(y_2\) минут?
Программа получает на вход числа \(x_1\), \(y_1\), \(a_1\), \(b_1\), \(x_2\), \(y_2\) в указанном порядке. Все числа целые. Числа \(x_1\), \(a_1\), \(x_2\) — от 0 до 23, числа \(y_1\), \(b_1\), \(y_2\) — от 0 до 59.
Выведите два числа \(a_2\) и \(b_2\), определяющие сколько будет времени на самом деле, когда на часах будет \(x_2\) часов \(y_2\) минут.
| Ввод | Вывод |
|---|---|
12 |
10 36 |
12 |
14 0 |
В григорианском календаре в году — 365 дней, кроме високосных лет, в которых на один день больше. Високосными годами являются года, которые делятся на 4, кроме годов, которые делятся на 100, среди них високосными являются только года, которые делятся на 400. То есть високосными были года 1600 и 2000, а года 1700, 1800, 1900 високосными не были.
Рассмотрим пролептический григорианский календарь, распространив указанные правила даже на те года, которые были до его введения. Вам дано число \(n\), определите количество дней в первых полных \(n\) годах календаря (в годах с номерами от 1 до \(n\)).
Программа получает на вход число \(n\), \(1\le n\le 10^4\).
Программа должна вывести одно целое число.
| Ввод | Вывод |
|---|---|
2024 |
739251 |
Остановки расположены вдоль улицы через каждые \(d\) метров, то есть на расстоянии \(d\), \(2d\), \(3d\) и т.д. Никомед решил прогуляться и пошёл домой от остановки рядом со школой пешком. Когда он прошёл \(s\) метров, то начался дождь. Определите расстояние, которое ему нужно пробежать, чтобы укрыться от дождя на ближайшей остановке.
Программа получает на вход целые числа \(d\) и \(s\) в разных строках.
Программа должна вывести одно число — искомое расстояние.
| Ввод | Вывод |
|---|---|
300 |
100 |
350 |
50 |
Часовые пояса нумеруются величиной различия местного времени с временем UTC. В часовом поясе UTC\(+A\) местное время больше, чем время в часовом поясе UTC\(+0\) на \(A\) часов (если же \(A\lt 0\), то меньше на \(|A|\) часов).
Например, если в часовом поясе UTC\(+0\) часы показывают 12 часов, то в часовом поясе UTC\(+1\) в этот момент 13 часов, а в часовом поясе UTC\(−1\) — 11 часов.
Мы будем считать, что значение \(A\) — целое число от -11 до 12. То есть мы не будем рассматривать такие часовые пояса, как UTC\(+13\), время в которой отличается от UTC\(-11\) ровно на сутки.
Ваш друг прислал вам сообщение, что у него сейчас часы показывают \(H_1\) часов, \(0\le H_1\le23\). Вы посмотрели на свои часы и обнаружили, что они показывают \(H_2\) часов, \(0\le H_2\le23\). Вы находитесь в часовом пояcе UTC\(+A\), \(-11\le A\le 12\). Определите, в каком часовом поясе находится ваш друг.
Программа получает на вход числа \(H_1\), \(H_2\), \(A\) и должна вывести номер часового пояса друга: число от \(-11\) до \(12\).
| Ввод | Вывод |
|---|---|
23 |
-2 |
Тесты к этой задаче закрытые.
\(N\) человек разбили на \(M\) команд, в каждой команде есть хотя бы один человек. Все члены каждой команды обменялись рукопожатиями. Посчитайте минимальное и максимальное число возможных рукопожатий.
Программа получает на вход числа \(N\) и \(M\), \(1 \le M\le N\) и должна вывести два числа — минимальное и максимальное число рукопожатий.
| Ввод | Вывод |
|---|---|
4 |
2 |
Тесты к этой задаче закрытые.
Напишите программу, которая считывает два целых числа \(a\) и \(b\) и выводит наибольшее значение из них.
При решении задачи можно пользоваться только
целочисленными арифметическими операциями +, -,
*, //, %, =.
Нельзя пользоваться нелинейными конструкциями: ветвлениями, циклами, функциями.
| Ввод | Вывод |
|---|---|
8 |
8 |
5 |
8 |
5 |
5 |
Тесты к этой задаче закрытые.
Имеется \(N\) кг металлического сплава. Из него изготавливают заготовки массой \(K\) кг каждая. После этого из каждой заготовки вытачиваются детали массой \(M\) кг каждая (из каждой заготовки вытачивают максимально возможное количество деталей). Если от заготовок после этого что-то остается, то этот материал возвращают к началу производственного цикла и сплавляют с тем, что осталось при изготовлении заготовок. Если того сплава, который получился, достаточно для изготовления хотя бы одной заготовки, то из него снова изготавливают заготовки, из них— детали и т.д.
Напишите программу, которая вычислит, какое количество деталей может быть получено по этой технологии из имеющихся исходно \(N\) кг сплава.
Программа получает на вход три натуральных числа \(N\), \(K\), \(M\), при этом \(K\ge M\), сами числа могут быть очень большими (пошаговое моделирование не получится).
Выведите одно число — количество деталей, которое может получиться по такой технологии.
| Ввод | Вывод |
|---|---|
10 |
4 |
13 |
3 |
14 |
4 |
13 |
2 |
1 |
0 |
Тесты к этой задаче закрытые.
Как известно, длину Удава можно измерять Попугаями и Мартышками. Оказалось, что длина Удава равна \(n\) целым Попугаям (и, возможно, ещё какая-то дробная часть Попугая) или \(m\) целым Мартышкам (и, возможно, ещё какая-то дробная часть Мартышки). Определите, какая минимальная и максимальная возможная длина Мартышки в Попугаях.
Программа получает на вход два целых числа \(n\) и \(m\), каждое на своей строке — количество Попугаев и Мартышек в Удаве, соответственно.
Программа должна вывести два целых числа — минимальную и максимальную возможную длину одной Мартышки в Попугаях.
| Ввод | Вывод |
|---|---|
38 |
6 |
Тесты к этой задаче закрытые.