Даны \(N\) натуральных чисел. Упорядочите их в порядке возрастания последней цифры числа, а при равенстве последней цифры — по возрастанию самих чисел. Упорядоченные числа выведите через пробел.
| Ввод | Вывод |
|---|---|
123 321 333 |
321 123 333 |
Однажды, неловкая секретарша перепутала личные дела учащихся. Теперь их снова необходимо упорядочить сначала по классам, а внутри класса по фамилиям.
В первой строке входных данных записано число \(N\) — количество личных дел. Далее записано \(N\) строк, каждая из которых состоит из фамилии учащегося (строка без пробелов) и номера класса (целое число от 1 до 11).
Нужно вывести список всех учащихся, сначала выводя номер класса, затем — фамилию учащегося. Список должен быть отсортирован по классу, а затем по фамилии.
Указание: составьте список из кортежей: номер класса и фамилия участника.
| Ввод | Вывод |
|---|---|
3 |
9 Petrov |
Мальчик Антон решает вступительную работу в летний математический лагерь. В ней \(N\) заданий, которые можно выполнять в произвольном порядке. Разные задачи требуют разного времени для решения в зависимости от их сложности. Пусть сложность \(i\)-го задания равна \(T_i\). Если задание с номером \(i\) выполнять \(j\)-м по счету, Антону потребуется \(T_i\times j\) времени: чем больше думаешь, тем больше устаешь. Например, если начать с первой задачи, а затем выполнить вторую, то потребуется \(T_1\times 1 + T_2\times2\) времени, а если выполнить сначала вторую задачу, а затем первую — то \(T_2\times 1 + T_1\times2\) . Подскажите Антону, в каком порядке нужно решать задачи, чтобы на выполнение всей работы ушло как можно меньше времени.
Единственная строка входных данных содержит \(N\) целых чисел \(T_1\), \(T_2\), ..., \(T_N\) через пробел — сложности данных задач.
Требуется вывести номера задач в том порядке, в котором их нужно решать, чтобы уложиться в минимальное время. Если решений несколько, нужно вывести любое из них.
| Ввод | Вывод |
|---|---|
2 3 |
2 1 |
Каждый из \(n\) выпускников магической школы получает посох силы \(a_i\) и кольцо силы \(b_i\). При этом уровень магической силы выпускника определяется отношением \(\frac{a_i}{b_i}\).
В распоряжении государственной экзаменационной комиссии есть \(s\) посохов и \(r\) колец. Комиссия хочет раздать выпускникам кольца и посохи так, чтобы суммарная магическая сила выпускников была бы максимальной.
Первая строка входных данных содержит три числа \(n\), \(s\), \(r\) (\(1\le n\le 10^5\), \(n\le s\le 10^5\), \(n\le r\le 10^5\)). Вторая строка содержит \(s\) чисел — магические силы посохов, третья строка содержит \(r\) чисел — магические силы колец. Все силы — целые, положительные, не превосходят \(10^6\).
Программа должна вывести \(n\) строк. \(i\)-я строка содержит два числа — номер посоха и номер кольца, которые получит \(i\)-й выпускник.
| Ввод | Вывод |
|---|---|
2 4 3 |
1 2 |
Али–Баба попал в пещеру, в которой находятся \(N\) предметов. У каждого предмета есть стоимость, при этом предметы могут быть бесполезными и даже вредными — их стоимость отрицательна. Али–Баба может унести не более \(M\) предметов. Определите, какие предметы следует выбрать Али–Бабе так, чтобы их стоимость была максимально возможной.
Первая строка входных данных содержит два числа \(N\) и \(M\) (\(0\le N\le 10^5\), \(0\le M\le 10^5\)) — количество предметов в пещере и количество предметов, которое может унести Али–Баба.
В следующей строке записаны \(N\) целых чисел \(a_i\) (\(-10^9\le a_i\le 10^9\)) — стоимости предметов в пещере.
Программа должна вывести не более \(M\) различных чисел от \(1\) до \(N\) — номера предметов, которые выберет Али–Баба.
| Ввод | Вывод |
|---|---|
7 3 |
1 2 4 |
На очередном уровне неважно какой компьютерной игры вам противостоят \(n\) драконов. У каждого дракона есть его сила \(s_i\) и бонус \(b_i\). Чтобы победить дракона, ваша сила должна быть больше, чем \(s_i\), а после победы над драконом ваша сила увеличивается на \(b_i\).
Первоначально ваша сила равна \(s\). Вы сами можете выбирать, в каком порядке вы будете побеждать драконов. Определите максимальное количество драконов, которое вы можете победить.
Первая строка входных данных содержит два числа: количество драконов \(n\) и начальное значение вашей силы \(s\). Далее следует \(n\) строк, каждая строка содержит два целых положительных числа \(s_i\) и \(b_i\), не превосходящих \(10^9\).
Программа должна вывести одно целое число — максимальное число драконов, которое вы можете победить.
Пояснение. В примере из условия ваша сила равна 10. Сначала нужно победить третьего дракона, после этого ваша сила станет равна 15. Затем нужно победить первого дракона, после этого ваша сила станет равна 20. Победить второго дракона не получится, потому что его сила также равна 20.
| Ввод | Вывод |
|---|---|
3 10 |
2 |
Дети в детском саду изучают английский алфавит. Они встают в круг и по очереди называют буквы. Первый ребенок в ряду громко называет первую букву алфавита — A. Второй должен назвать B, третий — C и так далее. Всего детей в группе, как и букв в английском алфавите, ровно 26.
Дети учат буквы подряд и каждый из них знает несколько первых букв алфавита. Кто-то, возможно, знает только букву A, кто-то буквы A, B, C, D, а кто-то может знать и весь алфавит. Ребёнок может назвать только ту букву, которую он знает.
Расставьте детей так, чтобы они могли назвать весь алфавит целиком, или определите, что это сделать нельзя.
Программа получает на вход строку из 26 заглавных букв английского алфавита. \(i\)-я буква этой строки обозначает, какую последнюю букву алфавита знает \(i\)-й ребёнок в группе.
Если можно расставить детей так, чтобы они назвали весь алфавит, выведите YES. В следующей строке выведите
перестановку чисел от 1 до 26 — порядковые номера детей в расстановке, позволяющей назвать им весь алфавит.
Если расставить детей невозможно, программа должна вывести одно слово NO.
| Ввод | Вывод |
|---|---|
ZYXWVUTSRQPONMLKJIHGFEDCBA |
YES |
YYYYYYYYYYYYYYYYYYYYYYYYYY |
NO |
На автобусную остановку каждую минуту подходит автобус одного из маршрутов. Вам даны номера маршрутов автобусов, отправляющихся по порядку в течение \(n\) минут.
Требуется определить максимально возможное время ожидания для пассажира, желающего уехать определенным маршрутом. При этом не учитываются пассажиры, которые приходят после отправления последнего автобуса данного маршрута, а также пассажиры, приходящие раньше отправления первого автобуса данного маршрута. То есть вам нужно найти самый длинный интервал между двумя автобусами одного маршрута.
Программа получает на вход число \(n\) (\(2\le n\le 10^5\)) . В следующей строке записаны \(n\) чисел \(a_i\) (\(1\le a_i\le 10^9\)) —номера автобусов в порядке отправления. Гарантируется, что любое значение в этом списке повторяется не менее двух раз.
Программа должна вывести одно число — максимальный интервал между двумя автобусами одного маршрута.
| Ввод | Вывод |
|---|---|
8 |
4 |
4 |
1 |
Есть распечатанный список имён, который забыли отсортировать перед печатью. Теперь мы хотим отсортировать его при помощи ножниц и скотча: можно разрезать список на несколько частей, переставить и склеить полученные части. Определите минимальное число разрезов, которое необходимо сделать для этого.
Список напечатан на одном листе бумаги, одно имя занимает одну строку.
Первая строка входных данных содержит одно целое число \(n\) (\(1\le n\le 10^5\)) — количество имён в списке. Следующие \(n\) строк содержат имена, по одному имени в строке. Имена могут состоять из заглавных и строчных английских букв, символов «.», «-» и пробела. Каждое имя содержит не более 20 символов. Имена сравниваются в лексикографическом порядке, символы сравниваются по ASCII-кодам.
Выведите одно число — минимальное число разрезов, которое необходимо выполнить для сортировки списка.
| Ввод | Вывод |
|---|---|
4 |
2 |
В этой задаче вам нужно научиться сортировать не числа, а рациональные дроби. Программа получает на вход \(N\) дробей: сначала задается число \(N\), потом идет \(N\) строк, в каждой из которых записана одна дробь. Дробь записана в виде \(a/b\), где \(a\) и \(b\) —натуральные числа.
Программа должна вывести список этих дробей в порядке неубывания. Если в списке есть две равные дроби \(a/b=c/d\), то раньше выводится дробь, у которой меньше числитель.
Указание. Составьте список из кортежей (\(a / b\), \(a\), \(b\)).
| Ввод | Вывод |
|---|---|
3 |
2/6 |
Ваш танк находится на краю поля боя, будем считать, что он стоит в центре координат. Поле боя простирается на восток и на нем находятся танки противников, которые будем считать точками с целочисленными координатами. Вы можете стрелять по прямой, и ваши бронебойные заряды уничтожают все танки противников, находящихся на линии выстрела. Определите, какое наименьшее число выстрелов необходимо для уничтожения всех танков противника.
Первая строка входных данных содержит количество танков \(N\le 10^5\). Следующие \(N\) строк содержат по два числа \(x_i\) и \(y_i\) — координаты танков (\(0\lt x_i\le 10^3\), \(-10^3\le y_i\le 10^3\)).
Программа должна вывести одно число — необходимое количество выстрелов \(K\). В следующей строке необходимо вывести \(K\) чисел от 1 до \(N\) — номера танков противника, по котором необходимо произвести выстрелы.
| Ввод | Вывод |
|---|---|
4 |
3 |
На командных олимпиадах по программированию, проводимых по правилам ICPC, команды в турнирной таблице упорядочены следующим образом:
Упорядочите результаты олимпиады по этим правилам.
Первая строка входных данных содержит количество команд \(n\) (\(1\le n\le 100\,000\)), участвовавших в турнире. Следующие \(n\) строк содержат результаты команд. В \(i\)-й строке записано два целых числа \(s_i\) (\(0\le s_i\le 100\)) — количество задач, решенных \(i\)-й командой и \(t_i\) (\(0\le t_i\le 100\,000\)) — штрафное время \(i\)-й команды.
Программа должна вывести \(n\) чисел от 1 до \(n\) — номера команд в порядке их следования в турнирной таблице.
| Ввод | Вывод |
|---|---|
5 |
5 2 1 3 4 |
Вы хотите купить себе ноутбук. У вас есть выбор — купить ноутбук подороже и помощнее или подешевле и послабее. Для начала вы хотите составить список имеющихся в продаже интересных ноутбуков.
В продаже есть \(n\) моделей ноутбуков. Каждый ноутбук характеризуется двумя числами: ценой \(p_i\) и мощностью \(s_i\). Все стоимости различны, все мощности также различны.
Назовём \(i\)-й ноутбук неинтересным, если существует ноутбук \(j\) такой, что \(p_j\lt p_i\), а \(s_j\gt s_i\), то есть ноутбук \(j\) будет дешевле и мощнее. Все остальные ноутбуки назовём интересными. То есть для интересных ноутбуков выполнено правило, что чем больше мощность, тем выше цена. Определите, какие модели ноутбуков являются интересными.
Программа получает на вход количество моделей ноутбуков \(n\) (\(1\le n\le 10^5\)). Следующие \(n\) строк содержат по два целых положительных числа \(p_i\) и \(s_i\), не превосходящих \(10^9\).
Программа должна вывести номера интересных ноутбуков в порядке возрастания.
| Ввод | Вывод |
|---|---|
4 |
2 4 |
Другая симпатичная и предприимчивая девушка ищет себе идеального партнера для танцев.
Идеальный кавалер по ее представлениями должен иметь рост 180 сантиметров, поэтому прежде всего она хочет найти юношу, чей рост как можно ближе к 180 сантиметрам. Будет ли кавалер выше или ниже указанной величины, не имеет значения (то есть юноши с ростом 179 и 181 сантиметр одинаково привлекательны).
Среди всех кандидатов одного роста ей нужен кто-то, чей вес насколько это возможно, близок к 75 килограмм, но не превышает этой величины. Если же все кандидаты одного роста весят более 75 килограмм, то девушка выберет самого легкого из них.
Вам дан список кавалеров, содержащий имя партнера, его рост и вес.
Отсортируйте список по критерию привлекательности роста, при равной привлекательности роста — по привлекательности веса. При одинаковых параметрах роста и веса список должен быть отсортирован в лексикографическом порядке.
Выведите отсортированный список (только имена кавалеров).
| Ввод | Вывод |
|---|---|
10 |
John |
Как известно, Россия была одним из ведущих экспортеров нефти. Разные страны мира, от достаточно больших до сравнительно маленьких, нуждаются в этой нефти как в воздухе. В ее состав в больших количествах входят ароматические углеводороды, которые обуславливают ее высокое качество. Доставка нефти в пункт назначения осуществляется с помощью нефтепровода. Считается, что количество нефти, отправленное в страну назначения, равно количеству полученной нефти. На самом деле это, конечно, не так. Как и многое другое, нефть воруют некоторые несознательные личности. Причем неофициально считается, что больше нефти воруют в нефтепроводах тех стран, куда нефти посылается больше (может быть, несознательные личности считают, что приносят, таким образом, меньше ущерба, кто знает...). Официальное руководство компании РусскаяНефть решило узнать, правдивый это слух или нет, чтобы усилить (а может просто установить) охрану на тех нефтепроводах, где больше всего воруют нефть.
Для этого им нужно отсортировать нефтепроводы по количеству нефти, которая протекает в направлении какой-то страны за сутки. У компании РусскаяНефть, как и у любой уважающей себя компании, есть несколько штатных программистов, и руководство предложило им решить эту, в сущности, нетрудную задачу. Но программистов поставило в тупик то, что данные о количестве нефти представлены в разных единицах измерения (начиная от граммов и заканчивая тоннами).
Поэтому они решили найти человека, который был бы в силах решить эту задачу за них, и обещают взять его на работу в эту перспективную и процветающую компанию. Решите задачу, и, кто знает, может, повезет именно Вам?
В первой строке входных данных находится целое число \(N\) (\(1\le N\le 1000\)) — количество нефтепроводов. В каждой из следующих \(N\) строк находится количество (точнее — масса) нефти, транспортированной по соответствующему нефтепроводу за сутки, по одному в строке. Масса нефти задана целым числом от 1 до 10000 с указанием соответствующей единицы измерения. Число и единица измерения разделены ровно одним пробелом. Единица измерения задается одной из трех букв: g (граммы), p (пуды), t (тонны), причем перед этой буквой может стоять одна из приставок: m (милли-), k (кило-), M (мега-), G (гига-). Напомним, что эти приставки обозначают умножение единицы измерения на 10-3, 103, 106 и 109 соответственно. 1 пуд = 16380 граммов, 1 тонна = 106 граммов.
Выведите \(N\) строк, в которых должны быть записаны массы нефти в порядке неубывания. Каждая строка должна описывать массу нефти в одном из нефтепроводов.
Масса должна быть описана согласно формату входного файла. Единицы измерения масс в выходном файле не обязаны соответствовать единицам измерения масс во входном файле, главное, чтобы массы были равны исходным. Все числа в выходном файле, также как и во входном, должны быть натуральными и не превышать 10000.
| Ввод | Вывод |
|---|---|
5 |
32 mg |
Вам дан массив из \(n\) целых различных чисел. Вам нужно его отсортировать, но вы можете выполнить один раз одну операцию: взять подотрезок этого массива и развернуть его в обратном порядке. Определите, сможете ли вы отсортировать массив при помощи такой операции.
Первая строка входных данных содержит целое число \(n\) (\(1\le n\le 10^5\)) — размер массива. Следующая строка содержит \(n\) различных целых положительных чисел \(a_i\), не превосходящих \(10^9\).
Если отсортировать массив при помощи одного разворота подотрезка можно, выведите слово YES.
В следующей строке выведите два числа \(l\) и \(r\) (\(1\le l\le r \le n\)) — номера первого и последнего
элемента разворачиваемого подотрезка массива.
Если отсортировать массив невозможно, выведите одно слово NO.
| Ввод | Вывод |
|---|---|
3 |
YES |
4 |
YES |
4 |
NO |
2 |
YES |
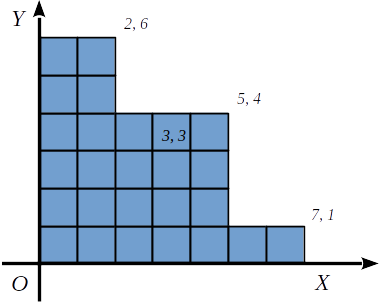
Даны \(n\) прямоугольников, стороны которых параллельны осям координат. Прямоугольники расположены в первой четверти и левый нижний угол каждого прямоугольника находится в начале координат.
Все прямоугольники покрасили. Определите площадь покрашенной фигуры.
Программа получает на вход количество прямоугольников \(n\) (\(1\le n\le 10^5\)). Следующие \(n\) строк содержат по два целых положительных числа \(x_i\) и \(y_i\), не превосходящих \(10^9\) — координаты правого верхнего угла прямогольника. Прямоугольники могут совпадать.
Программа должна вывести одно число — площадь объединения данных прямоугольников.
Картинка соответствует примеру из условия.

| Ввод | Вывод |
|---|---|
4 |
26 |