Упражнения

В задачах этого листка на проверку необходимо сдать только тело функции. Внутри функции не должно быть вызова turtle.mainloop(). Можно (и рекомендуется) использовать вспомогательные функции.

Также в вашем решении не должно быть строки типа import turtle и вызова метода speed черепашки.

Первым параметром является номер итерации построения фрактала n. Как правило, начальным значением является \(n=0\), но в некоторых задачах начальной итерацией является \(n=1\). Вторым параметром является размер фрактала size. Фракталы, с равным значением size, должны иметь равные размеры и располагаться в одном месте, то есть при изменении n фрактал не должен увеличиваться в размерах или “перепрыгивать” в другое место.

A: Снежинка Коха

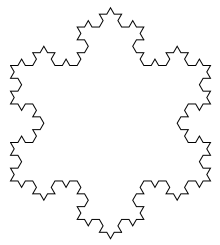
Напишите функцию draw_koch_snowflake(n, size), которая рисует снежинку Коха — замкнутую ломаную, составленную из трёх кривых Коха. n — номер итерации кривой Коха, size — расстояние между концами одной кривой Коха.

Вызов функции Результат работы 
draw_koch_snowflake(0, 200)
 
draw_koch_snowflake(1, 200)
 
draw_koch_snowflake(2, 200)
 
draw_koch_snowflake(3, 200)

B: Квадратная кривая Коха

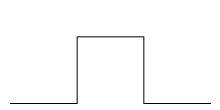
Напишите функцию draw_quadratic_koch_curve(n, size), которая рисует квадратную кривую Коха. n — номер итерации кривой, size — расстояние между концами одной кривой. Нулевая итерация — отрезок длины size. Каждая последующая итерация получается из предыдущей итерации заменой одного отрезка на 5 меньших равных отрезков.

При изменении значения \(n\) концы кривой должны находиться в одних и тех же точках, а расстояние между концами должно быть равно size.

Вызов функции Результат работы 
draw_quadratic_koch_curve(0, 200)
 
draw_quadratic_koch_curve(1, 200)
 
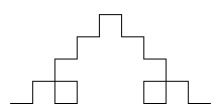
draw_quadratic_koch_curve(2, 200)
 
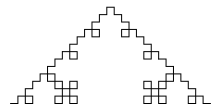
draw_quadratic_koch_curve(3, 200)

C: Кривая Минковского

Напишите функцию draw_minkowski_curve(n, size), которая рисует n-ю итерацию кривой Минковского. Нулевая итерация — отрезок длины size. Каждая последующая итерация получается из предыдущей итерации заменой одного отрезка на 8 меньших равных отрезков.

При изменении значения \(n\) концы кривой должны находиться в одних и тех же точках, а расстояние между концами должно быть равно size.

Вызов функции Результат работы 
draw_minkowski_curve(0, 200)
 
draw_minkowski_curve(1, 200)
 
draw_minkowski_curve(2, 200)
 
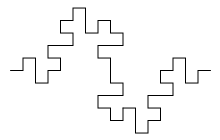draw_minkowski_curve(3, 200)

D: Кривая Леви

Напишите функцию draw_levy_curve(n, size), которая рисует n-ю итерацию кривой Леви. Нулевая итерация — отрезок длины size. Каждая последующая итерация получается из предыдущей итерации заменой одного отрезка на 2 меньших отрезка, являющихся катетами равнобедренного прямоугольного треугольника, построенного на данном отрезке, как на гипотенузе.

При изменении значения \(n\) концы кривой должны находиться в одних и тех же точках, а расстояние между концами должно быть равно size.

В примерах красным цветом нарисована \(n-1\)-я итерация кривой Леви, её рисовать не надо.

Обратите внимание, для того, чтобы эта конструкция работала, необходимо, чтобы после вызова рекурсивной функции черепашка всегда была ориентирована, как будто бы ей передали значение \(n=0\), то есть если \(n\gt0\), то после выполнения рекурсивных вызовов и перемещения в конечную точку необходимо будет ещё повернуть черепашку так, чтобы вернуть её первоначальную ориентацию. Иными словами, необходимо добиться того, чтобы при вызове фукнции с любым значением \(n\) (прежде всего проверьте \(n=0\), \(n=1\), \(n=2\)) черепашка смещалась на расстояние size, при этом её ориентация после выполнения алгоритма не меняется.

Вызов функции Результат работы 
draw_levy_curve(0, 100)
 
draw_levy_curve(1, 100)
 
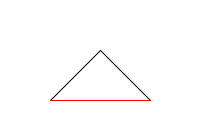draw_levy_curve(2, 100)
 
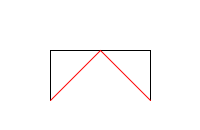draw_levy_curve(3, 100)
 
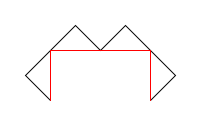draw_levy_curve(4, 100)
 
draw_levy_curve(10, 100)

E: Дерево

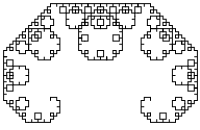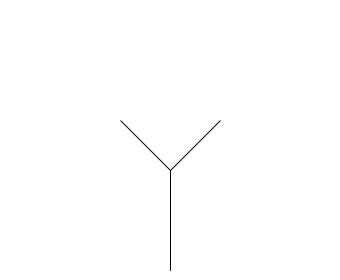
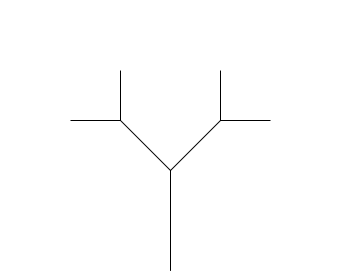
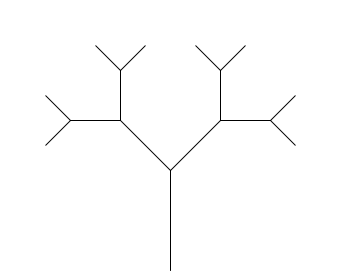
Напишите функцию draw_tree(n, size), которая рисует «дерево» с n развилками.

Дерево при \(n=0\) представляет собой отрезок длины size (ствол). Дерево при \(n\gt 0\) — это отрезок длины size, от которого под углом в \(45^\circ\) отходят два дерева с \(n-1\) развилками и стволами длины в \(\sqrt{2}\) раз меньше.

У двух деревьев, которые различающися значением \(n\), должна быть общая часть, совпадающая с тем деревом, у которого \(n\) меньше.

При изменении значения \(n\) концы кривой должны находиться в одних и тех же точках, а расстояние между концами должно быть равно size.

Вы можете нарисовать дерево, ствол которого направлен в направлении черепахи (то есть по умолчанию — вправо, а не вверх). В примерах ниже черепаха поворачивается перед вызовом функции draw_tree.

В этой задаче необходимо, чтобы при любом вызове рекурсивной функции было нарисовано нужное дерево, а черепашка в результате исполнения функции возвращалась в исходную точку с сохранением исходной ориентации.

Вызов функции Результат работы 
turtle.left(90)
draw_tree(0, 100)
 
turtle.left(90)
draw_tree(1, 100)
 
turtle.left(90)
draw_tree(2, 100)
 
turtle.left(90)
draw_tree(3, 100)
 
turtle.left(90)
draw_tree(5, 100)

F: Ветка

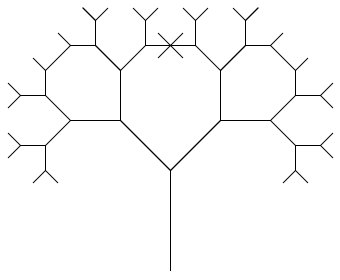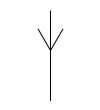
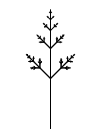
Напишите функцию draw_branch(n, size, angle, coeff1, coeff2), которая рисует «ветку», у которой \(n\) развилок.

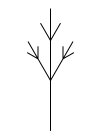
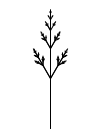
Ветка при \(n=0\) представляет собой отрезок длины size (длина основания). Ветка при \(n\gt 0\) — это основание длины size, от которого отходят три ветки, у которых \(n\) меньше на \(1\). Вперёд отходит ветка с длиной основания size * coeff1. В стороны отходят ветки с длиной основания size * coeff2. Боковые ветки повёрнуты под углом angle к основанию.

Вызов функции Результат работы 
turtle.left(90)
draw_branch(0, 50, 30, 0.8, 0.4)
 
turtle.left(90)
draw_branch(1, 50, 30, 0.8, 0.4)
 
turtle.left(90)
draw_branch(2, 50, 30, 0.8, 0.4)
 
turtle.left(90)
draw_branch(3, 50, 30, 0.8, 0.4)
 
turtle.left(90)
draw_branch(5, 50, 30, 0.8, 0.4)
 
turtle.left(90)
draw_branch(5, 50, 30, 0.8, 0.3)
 
turtle.left(90)
draw_branch(5, 50, 30, 0.6, 0.3)
 
turtle.left(90)
draw_branch(5, 50, 45, 0.6, 0.3)

G: Треугольный ковёр Серпинского

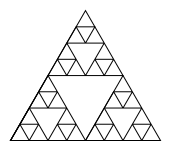
Напишите функцию draw_sierpinski_triangle(n, size), которая рисует треугольный ковёр Серпинского.

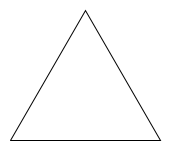
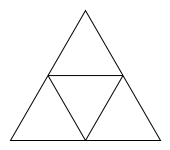
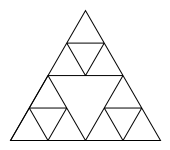
Фрактал при \(n=0\) представляет собой правильный треугольник со стороной size. Затем треугольник делится на 4 меньших треугольника, и выбрасывается средний треугольник. Этот процесс повторяется с каждым получившимся треугольником.

Вызов функции Результат работы 
draw_sierpinski_triangle(0, 150)
 
draw_sierpinski_triangle(1, 150)
 
draw_sierpinski_triangle(2, 150)
 
draw_sierpinski_triangle(3, 150)

H: Кривая Серпинского

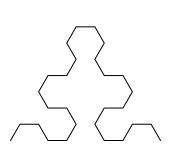
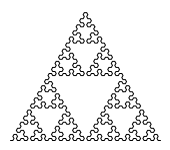
Напишите функцию draw_sierpinski_curve(n, size), которая рисует треугольную кривую Серпинского.

Фрактал при \(n=0\) представляет собой отрезок длины size. На каждой следующей итерации отрезок заменяется на три отрезка вдвое меньшей длины.

При изменении значения \(n\) концы кривой должны находиться в одних и тех же точках, а расстояние между концами должно быть равно size.

Обратите внимание, что сторона, в которую направлены части кривой, меняются — посмотрите, как строится кривая при \(n=2\). Поэтому для решения задачи вам понадобится ещё одна функция, которая строит кривую Серпинского, но отражённую в другую сторону.

Другим возможным подходом является передача в функцию дополнительного параметра, который задаёт направление кривой: def draw_sierpinski_curve(n, size, orientation=1). Параметр orientation может принимать значения 1 или -1, если он не задан (как при запуске в тестирующей системе), то он будет равен 1.

Вызов функции Результат работы 
draw_sierpinski_curve(0, 150)
 
draw_sierpinski_curve(1, 150)
 
draw_sierpinski_curve(2, 150)
 
draw_sierpinski_curve(3, 150)
 
draw_sierpinski_curve(6, 150)

I: Кривая дракона

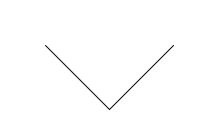
Напишите функцию draw_dragon_curve(n, size), которая рисует кривую дракона.

Фрактал при \(n=0\) представляет собой отрезок длины size. Каждая следующая итерация кривой представляет собой две уменьшенные копии кривой, повёрнутые на \(90^\circ\). Направление поворота должно быть точно таким, как в примерах.

При изменении значения \(n\) концы кривой должны находиться в одних и тех же точках, а расстояние между концами должно быть равно size.

При решении задачи вам понадобится реализация дополнительной функции, рисующая кривую дракона, получаемую при прохождении в обратном направлении. Другим возможным подходом является передача в функцию дополнительного параметра, который задаёт направление кривой: def draw_dragon_curve(n, size, orientation=1).

Вызов функции Результат работы 
draw_dragon_curve(0, 128)
 
draw_dragon_curve(1, 128)
 
draw_dragon_curve(2, 128)
 
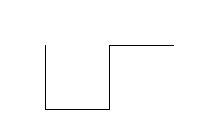draw_dragon_curve(3, 128)
 
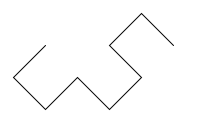draw_dragon_curve(4, 128)
 
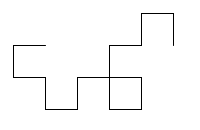draw_dragon_curve(9, 128)

J: Фрактал из квадратов

Напишите функцию draw_squares(n, size), которая рисует фракталов из квадратов размером size, size / 2, size / 4.

При \(n=0\) программа рисует квадрат со стороной size. Каждая следующая итерация получается из предыдущей итерации добавлением к каждому свободному углу квадрата нового квадрата, размер которого в два раза меньше.

Вызов функции Результат работы 
draw_squares(0, 64)
 

draw_squares(1, 64)
 

draw_squares(2, 64)
 

draw_squares(3, 64)

K: Центры масс треугольников

Напишите функцию draw_triangle_mass_center(n, size).

При \(n=0\) программа рисует правильный треугольник со стороной size. Каждая следующая итерация получается из предыдущей итерации разбиением каждого треугольника на три треугольника, соединяя вершины треугольника с центром его масс.

Если треугольник имеет вершины с координатами \((x_1, y_1)\), \((x_2, y_2)\), \((x_3, y_3)\), то его центр масс (точка пересечения медиан) имеет координаты \(x=\frac{x_1+x_2+x_3}{3}\), \(y=\frac{y_1+y_2+y_3}{3}\). Поэтому в этой задаче нужно работать с координатами, и вам понадобится вспомогательная функция, в которую нужно передавать координаты вершин треугольника.

Вызов функции Результат работы 
draw_triangle_mass_center(0, 200)
 
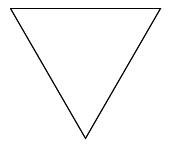draw_triangle_mass_center(1, 200)
 
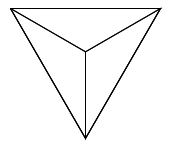draw_triangle_mass_center(2, 200)
 
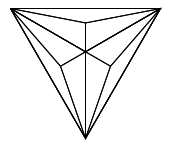draw_triangle_mass_center(3, 200)

L: Кривая Пеано

Напишите функцию draw_peano_curve(n, size), которая рисует кривую Пеано.

Функция должна нарисовать границу квадрата со стороной size, а внутри него нарисовать n-ю итерацию кривой Пеано. Поэтому вам понадобится минимум одна (а может быть и две) вспомогательная функция.

Мысленно разобьём квадрат на четыре меньших квадрата. Первая итерация кривая Пеано состоит из трёх отрезков, соединяющих середины этих квадратов. Каждая последующая итерация кривой Пеано состоит из четырёх меньших кривых Пеано, вписанных в эти квадраты, концы которых соединены тремя отрезками.

В пределе кривая Пеано заполняет весь квадрат (проходит через каждую точку квадрата).

Вызов функции Результат работы 
draw_peano_curve(1, 128)
 
draw_peano_curve(2, 128)
 
draw_peano_curve(3, 128)
 
draw_peano_curve(4, 128)

M: Квадратная кривая Серпинского

Напишите функцию draw_sierpinski_square(n, size), которая рисует квадратную кривую Серпинского.

Функция должна нарисовать границу квадрата со стороной size, а внутри него нарисовать n-ю итерацию кривой Серпинского. Поэтому вам понадобится минимум одна (а может быть и две) вспомогательная функция.

Кривая \(i\)-го порядка состоит из горизонтальных, вертикальных и диагональных отрезков. Длины вертикальных и горизонтальных отрезков — \(1/2^{i+2}\), диагональный отрезок имеет проекции \(1/2^{i+3}\) на обе оси координат.

В примерах красным цветом нарисована \(n-1\)-я итерация кривой, её рисовать не надо.

Вызов функции Результат работы 
draw_sierpinski_square(1, 256)
 
draw_sierpinski_square(2, 256)
 
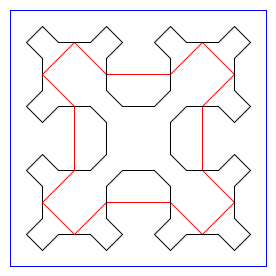draw_sierpinski_square(3, 256)
 
draw_sierpinski_square(4, 256)
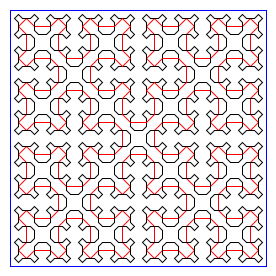