Упражнения

В задачах этого листка на проверку необходимо сдать только тело функции. Внутри функции не должно быть вызова turtle.mainloop(). Можно (и рекомендуется) использовать вспомогательные функции.

Также в вашем решении не должно быть строки типа import turtle, а также вызова метода speed черепашки.

A: Серединный треугольник

Напишите функцию draw_medial_triangle(size), которая рисует правильный треугольник со стороной size и проводит в нём срединные линии.

Вызов функции	Результат работы
draw_medial_triangle(100)

B: Вложенные треугольники

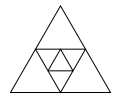
Напишите функцию draw_triangles(n, size), которая рисует последовательность из n вложенных правильных треугольников. Самый большой треугольник имеет сторону size, каждый следующий треугольник соединяет середины сторон большего треугольника.

Вызов функции	Результат работы
draw_triangles(3, 100)

C: Глаз дракона

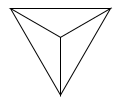
Напишите функцию draw_eye_of_dragon(size), которая рисует символ «Глаз дракона» — правильный треугольник со стороной size и горизонтальной верхней стороной, вершины которого соединены с центром треугольника.

Вызов функции	Результат работы
draw_eye_of_dragon(100)

D: Вложенные многоугольники

Напишите функцию draw_polygons(n, size), которая рисует последовательность из \(n-2\) вложенных правильных многоугольников с \(3\), \(4\), ..., \(n\) сторонами, с общей стороной. Длина каждой стороны равна size.

Вызов функции	Результат работы
draw_polygons(6, 100)

E: Полигональный цветок

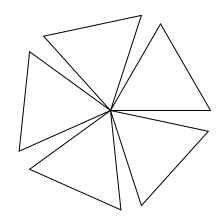
Напишите функцию draw_flower(n, k, size), которая рисует «цветок» с k лепестками (\(k\ge 2\)). Каждый лепесток является правильным n-угольником (\(n\ge3\)) со стороной size. Все лепестки имеют общую вершину, относительно которой они повёрнуты на равные углы.

Вызов функции	Результат работы
draw_flower(3, 5, 100)
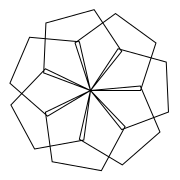
draw_flower(5, 7, 50)

F: Звёзды

Напишите функцию draw_star(n, k, size), которая рисует звёздочку — ломаную c n вершинами (\(n\ge3\)). Каждая вершина соединена с двумя вершинами: \(k\)-й в порядке обхода по часовой стрелке от этой вершины и \(k\)-й в порядке обхода против часовой стрелки от этой вершины, \(1\le k \lt n/2\). Например, если \(k=1\), то каждая вершина соединена с двумя соседними и звёздочка становится правильным \(n\)-угольником. Гарантируется что \(n\) и \(k\) взаимно просты, что означает, что звёздочка состоит из одной замкнутной ломаной. Длина каждого отрезка ломаной равна size.

Вызов функции	Результат работы
draw_star(5, 1, 100)
draw_star(5, 2, 200)
draw_star(8, 3, 200)

G: Полигональная спираль

Напишите функцию draw_spiral(n, k, coeff, angle, size), которая рисует спираль из n-угольников, закрученных по часовой стрелке и имеющих общий угол. Сторона первого многоугольника равна size, сторона каждого последующего многоугольника получается из стороны предыдущего многоугольника умножением на действительное число coeff, также следующий многоугольник повёрнут на угол angle по часовой стрелке. Общее число многоугольников равно k.

Вызов функции	Результат работы
draw_spiral(3, 50, 0.98, 10, 100)
draw_spiral(4, 50, 0.95, 20, 100)
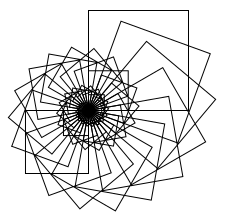
draw_spiral(3, 5, 1, 72, 50)
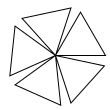
draw_spiral(6, 18, 1, 20, 50)
draw_spiral(3, 50, 1.02, 10, 50)

H: Треугольная сетка

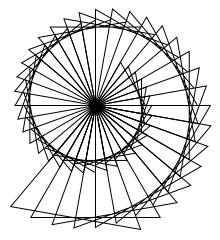
Напишите функцию draw_triangles(n, size), которая рисует правильный треугольник, разделённый по каждой стороне на n меньших трегольников. Длина стороны каждого маленького треугольника равна size.

Вызов функции	Результат работы
draw_triangles(5, 30)

I: Шестиугольная сетка

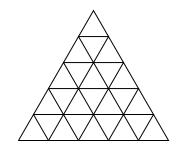
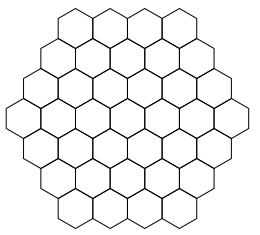
Напишите функцию draw_hexes(n, size), которая рисует шестиугольник, составленный из правильных маленьких шестиугольников. Вдоль каждой стороны большого шестиугольника размещается n маленьких шестиугольников. Длина стороны каждого маленького шестиугольника равна size.

Вызов функции	Результат работы
draw_hexes(4, 20)

J: Звёзды —2

Напишите функцию draw_star(n, k, size), которая рисует звёздочку — ломаную c n вершинами (\(n\ge3\)). Каждая вершина соединена с двумя вершинами: \(k\)-й в порядке обхода по часовой стрелке от этой вершины и \(k\)-й в порядке обхода против часовой стрелки от этой вершины, \(1\le k \lt n/2\). Все вершины образуют правильный n-угольник со стороной size.

В отличие от задачи «Звёзды», в этой задаче значения \(n\) и \(k\) не обязательно взаимно простые, поэтому в этой задаче изображение звезды может состоять из нескольких замкнутых ломаных. Кроме того, определение параметра size отличается, в этой задаче у всех звёзд с равным значением n и size позиции вершин звезды будут одинаковыми.

Указание. Вообще для решения этой задачи нужно знание тригонометрии, но можно воспользоваться самой черепашкой. Сначала, не опуская пера черепашки, пройдитесь по всем вершинам правильного n-угольника, и запомните координаты его вершин в списке, используя метод pos() черепашки. Затем, используя метод goto, нарисуйте отрезки, соединяющие нужные вершины.

Вызов функции	Результат работы
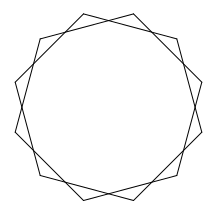
draw_star(12, 2, 50)
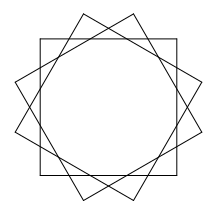
draw_star(12, 3, 50)
draw_star(12, 4, 50)
draw_star(12, 5, 50)