Дано целое число \(n\ge 0\). Вычислите сумму чисел \(0 + 1 + ... + n\) не используя формулу суммы арифметической прогрессии и циклы.
Решение оформите в виде рекурсивной функции sum0n(n),
получающей в качестве параметра значение \(n\) и возвращающей нужную сумму.
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
sum0n(5) |
15 |
Дано целое число \(n\gt 0\). Посчитайте сумму его цифр, не используя строковые операции
и циклы. Решение оформите в виде рекурсивной функции sum_of_digits(n),
возвращающей сумму цифр числа \(n\).
На проверку сдайте только тело функции.
Указание. Отбросьте от числа последнюю цифру, тем самым сведите задачу к меньшему числу.
| Вызов функции | Возвращаемое значение |
|---|---|
sum_of_digits(179) |
17 |
Дано целое число \(n\gt 0\). Определите, не используя строковые операции
и циклы. Решение оформите в виде рекурсивной функции min_digit(n),
возвращающей значение минимальной цифры числа \(n\). На проверку сдайте только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
min_digit(179) |
1 |
Дано целое число \(n\gt 0\). Определите не используя циклы, является ли это число точной степенью числа 2.
Решение оформите в виде рекурсивной функции is_power2(n),
возвращающей значение типа bool. Для чисел 1, 2, 4, 8 и т.д. функция
должна возвращать True, для остальных чисел — False.
На проверку сдайте только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
is_power2(8) |
True |
is_power2(3) |
False |
Последовательность Фибоначчи определяется так: \[ \cases{\varphi_0=0, \cr \varphi_1=1, \cr \varphi_{n}=\varphi_{n-1}+\varphi_{n-2} \mbox{, при } n \gt 1.} \]
Напишите рекурсивную функцию fib(n), которая по данному целому неотрицательному n
возвращает \(n\)-e число Фибоначчи.
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
fib(6) |
8 |
Вычислите число сочетаний \(\text{C}_n^k\) используя рекуррентое соотношение \[ \text{C}_n^k=\text{C}_{n-1}^{k-1}+\text{C}_{n-1}^{k} \]
Решение оформите в виде рекурсивной функции combination(n, k),
где \(0\le k \le n\).
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
combination(7, 3) |
35 |
Запустите программы, вычисляющие числа Фибоначчи при помощи рекурсивного и нерекурсивного алгоритма. Сравните время их работы для n=10, 20, 30, 40, 50.
Вычислите \(\text{C}_{20}^{10}\), \(\text{C}_{22}^{11}\), \(\text{C}_{24}^{12}\), \(\text{C}_{26}^{13}\) используя решение из предыдущей задачи.
Объясните результат.
Сделаем такое преобразование. \[ \text{C}_n^k = \dfrac{n!}{k!(n-k)!}=\dfrac{n\cdot(n-1)!}{k\cdot (k-1)!(n-k)!}=\frac{n}{k}\text{C}_{n-1}^{k-1}. \]
Вычислите число сочетаний \(\text{C}_n^k\) используя полученное рекуррентное соотношение.
Решение оформите в виде рекурсивной функции combination(n, k).
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
combination(7, 3) |
35 |
Сравните скорость двух функций, вычисляющих число сочетаний. Объясните полученный результат.
Можно написать рекурсивную функцию возведения в степень.
def power(a, n):
if n == 0:
return 1
return a * power(a, n - 1)
Такая функция имеет сложность \(O(n)\). Но возводить в степень можно гораздо быстрее, чем за \(n\) умножений. Для этого нужно воспользоваться следующими рекуррентными соотношениями:
\(a^n=(a^2)^{n/2}\) при четном \(n\),
\(a^n=a\cdot a^{n-1}\) при нечетном \(n\).
Реализуйте алгоритм быстрого возведения в степень. Если вы все сделаете правильно, то сложность вашего алгоритма будет \(O(\log n)\).
Решение оформите в виде функции power(a, n), где \(n\ge 0\). Использовать
стандартную функцию pow и оператор ** запрещается.
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
power(1.000000001, 1000000000) |
2.718282030814511 |
Для быстрого вычисления наибольшего общего делителя двух чисел используют алгоритм Евклида. Он построен на следующем соотношении: \(НОД(a,b)=НОД(a\bmod b,b)\).
Реализуйте рекурсивный алгоритм Евклида в виде функции gcd(a, b), возвращающей искомое значение.
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
gcd(12, 16) |
4 |
Напишите функцию product(a),
которая по данному списку чисел возвращает произведение
элементов данного списка, не используя циклы.
Список содержит только числа, но может быть пустым.
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
product([1, 7, 9]) |
63 |
Напишите рекурсивную функцию print_numbers(n),
которая выводит на экране целые числа от 1 до \(n\),
по одному числу в строке. Циклы и генераторы списков использовать нельзя.
Функция не должна возвращать значение.
Указание. Число \(n\) является параметром. Как свести задачу “вывести числа от 1 до \(n\)” к задаче с меньшим значением параметра?
Сдайте на проверку только тело функции.
| Вызов функции | Вывод |
|---|---|
print_numbers(3) |
1 |
Напишите рекурсивную функцию print_numbers(a, b),
которая выводит на экране целые числа от \(a\) до \(b\),
по одному числу в строке. Если \(a\lt b\), то числа выводятся
в порядке возрастания, если \(a\gt b\) — в порядке убывания.
Циклы и генераторы списков использовать нельзя. Функция не должна возвращать значение.
Сдайте на проверку только тело функции.
| Вызов функции | Вывод |
|---|---|
print_numbers(3, 6) |
3 |
print_numbers(7, 4) |
7 |
Напишите рекурсивную функцию read(),
не получающей параметров и не возвращающей значения.
Вызов этой функции должен приводить к считыванию со стандартного ввода чисел, до тех пор, пока не будет введено число, равное 0. При этом функция должна выводить на экран считанное число, если оно является нечётным.
Указание. При считывании нуля функция должна завершить работу. Иначе функция считывает число, выводит его на экран, если оно нечётное, а потом рекурсивно вызывает себя же.
В решении нельзя использовать циклы. Сдайте на проверку только тело функции.
| Вызов функции | Ввод | Вывод |
|---|---|---|
read() |
179 |
179 |
Напишите рекурсивную функцию read(),
не получающую параметров и возвращающую значение типа int.
Вызов этой функции должен приводить к считыванию со стандартного ввода чисел, до тех пор, пока не будет введено нечётное число. Функция должна вернуть это число.
В решении нельзя использовать циклы. Сдайте на проверку только тело функции.
| Вызов функции | Ввод | Возвращаемое значение |
|---|---|---|
read() |
10 |
179 |
Напишите рекурсивную функцию read(),
не получающей параметров и возвращающей список чисел типа int.
Вызов этой функции должен приводить к считыванию со стандартного ввода чисел, до тех пор, пока не будет введён ноль. Функция должна вернуть список всех считанных чисел, кроме последнего нуля.
В решении нельзя использовать циклы. Сдайте на проверку только тело функции.
| Вызов функции | Ввод | Возвращаемое значение |
|---|---|---|
read() |
1 |
[1, 2, 3] |
Дана последовательность целых чисел, заканчивающаяся числом 0. Выведите эту последовательность в обратном порядке. Сделайте это без использования списков и циклов.
Решение оформите в виде функцииreverse(),
не принимающей параметров, которая считывает со стандартного ввода
последовательность чисел до появления числа 0 и выводит эту же последовательность
в обратном порядке. Функция должна считать одно число и, если это число не 0, вызвать
себя рекурсивно.
Сдайте на проверку только тело функции.
| Вызов функции | Ввод | Вывод |
|---|---|---|
reverse() |
1 |
0 |
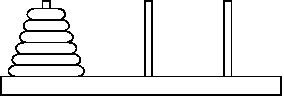
Головоломка “Ханойские башни” состоит из трех стержней, пронумерованных числами 1, 2, 3. На стержень 1 надета пирамидка из \(n\) дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного стержня на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку со стержня 1 на стержень 3 за минимальное число перекладываний.
Напишите функцию, которая решает головоломку; для данного числа дисков n
печатает последовательность перекладываний в формате
a b c, где a — номер перекладываемого диска,
b — номер стержня с которого снимается данный диск,
c — номер стержня на который надевается данный диск.
Например, строка 1 2 3 означает перемещение диска номер 1 со стержня
2 на стержень 3. В одной строке печатается одна команда.
Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.
Программа должна вывести минимальный (по количеству произведенных операций) способ перекладывания пирамидки из данного числа дисков.

Указание: подумайте, как переложить пирамидку из одного диска? Из двух дисков? Из трех дисков? Из четырех дисков? Пусть мы научились перекладывать пирамидку из \(n\) дисков с произвольного стержня на любой другой, как переложить пирамидку из \(n+1\) диска, если можно пользоваться решением для \(n\) дисков.
Решение оформите в виде функции move(n, start, finish),
которая печатает последовательность перекладываний дисков для перемещения
пирамидки высоты n со стержня номер start
на стержень номер finish.
Сдайте на проверку только тело функции.
В примере ниже пирамидка из 2 дисков перекладывается со стержня 1 на стержень 3.
| Вызов функции | Вывод |
|---|---|
move(2, 1, 3) |
1 1 2 |
Постановлением ЮНЕСКО оригинал Ханойской башни был подвергнут реставрации. В связи с этим во время пользования головоломкой нельзя было перекладывать кольца с первого стержня сразу на третий и наоборот.
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
В этой и последующих задачах про Ханойские башни на проверку необходимо сдать программу полностью.
| Ввод | Вывод |
|---|---|
1 |
1 1 2 |
2 |
1 1 2 |
На дорогах Ханоя было введено одностороннее круговое движение, поэтому теперь диск со стержня 1 можно перекладывать только на стержень 2, со стержня 2 на 3, а со стержня 3 на 1.
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
1 |
1 1 2 |
2 |
1 1 2 |
В Ханое несправедливо запретили класть самый маленький диск (номер 1) на средний колышек (номер 2).
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
2 |
1 1 3 |
Первоначально все диски лежат на стержне номер 1. Переместите диски с нечетными номерами на стержень номер 2, а с четными номерами - на стержень номер 3.
Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
2 |
1 1 2 |
3 |
1 1 2 |
Как и в предыдущих задачах, дано три стержня, на первом из которых надето \(n\) дисков различного размера. Необходимо их переместить на стержень 3 по следующим правилам:
Самый маленький диск (номер 1) можно в любой момент переложить на любой стержень.
Перемещение диска номер 1 со стержня a на стержень b
будем обозначать 1 a b.
Можно поменять два диска, лежащих на вершине двух стержней, если размеры этих дисков
отличаются на 1. Например, если на вершине стержня с номером a лежит
диск размером 5, а на вершине стержня с номером b лежит диск размером
4, то эти диски можно поменять местами. Такой обмен двух дисков будем обозначать
0 a b (указываются номера стержней, верхние диски которых обмениваются местами).
Для данного числа дисков \(n\), не превосходящего 10, найдите решение головоломки. вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000.
| Ввод | Вывод |
|---|---|
1 |
1 1 3 |
2 |
1 1 3 |
Поговорим о фракталах.
Последовательность Туе–Морса — это бесконечная последовательность из нулей и единиц, которая выглядит следующим образом:
01101001100101101001011001101001...
Строится она следующим образом. Последовательность начинается с числа 0. Затем повторяются следующие шаги: уже выписанная последовательность чисел повторяется, но при этом числа 0 меняются на 1, а числа 1 меняются на 0. То есть к число 0 будет дописано 1, а к ним будет дописано 10, получится 0110. К ним будет дописано 1001, получится 01101001 и т.д.
Пронумеруем элементы последовательности начиная с 0, то есть \(t_0=0\), \(t_1=1\), \(t_2=1\), \(t_3=0\) и т.д.
По данному значению \(i\) определите \(t_i\), то есть значение \(i\)-го символа последовательности. Значение \(i\) может быть очень большим, построить явно всю последовательность до \(i\)-го символа не получится.
Решение оформите в виде функции thue_morse(i), получающей в качестве параметра
значение \(i\) и возвращающей число 0 или 1.
| Вызов функции | Возвращаемое значение |
|---|---|
thue_morse(0) |
0 |
thue_morse(16) |
1 |
Кривая дракона — один из наиболее известных фракталов. Она строится так: на первом шаге проводится отрезок из начала координатной плоскости в точку (0; 1). Далее на каждом шаге из конца фрактала повторяется уже нарисованная часть фигуры, повернутая на 90 градусов против часовой стрелки
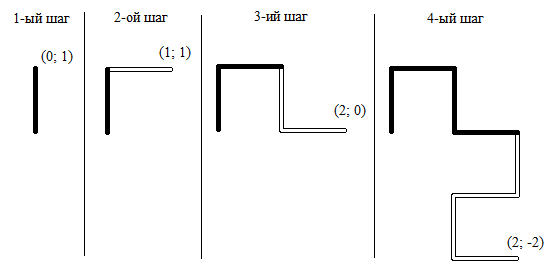
Рассмотрим кривую дракона на шаге номер \(n\ge 2\). Вы движетесь из точки (0, 0) и выписываете направления поворотов после прохождения каждого отрезка. Поворот направо обозначается буквой R, поворот налево — буквой L. Постройте последовательность поворотов.
Решение оформите в виде функции dragon(n), получающей в качестве
параметра число \(n\ge 2\) и возвращающей строку из букв L и R.
Сдайте на проверку тело функции (возможно использование и вспомогательных функций).
| Вызов функции | Возвращаемое значение |
|---|---|
dragon(3) |
"RRL" |
dragon(4) |
"RRLRRLL" |
Головоломка “Spin Out” (можно взять в 216 кабинете) представляет собой красную полоску, которую необходимо вытащить из серого футляра. На полоске размещены \(n\) дисков с рукоятками. Пронумеруем их числами от 1 до \(n\) слева направо. Каждый диск может находиться в вертикальном или горизонтальном положении.
Головоломка устроена так, что можно повернуть (то есть сделать диск вертикальным, если он был горизонтальным, или сделать диск горизонтальным, если он был вертикальным) два диска: самый левый диск (диск с номером 1) или диск, следующий за самым левым вертикальным диском (то есть диск, номер которого на 1 больше, чем минимальный номер вертикального диска).
Напишите программу, которая переводит \(n\) дисков из горизонтального положения в вертикальное.
Программа получает на вход количество дисков в головоломке \(N\) \((1\le N\le 10)\).
Программа должна вывести последовательность номеров дисков, с которыми совершается действие. Если диск номер \(i\) поворачивается вертикально, то программа выводит число \(i\). Если диск номер \(i\) поворачивается горизонтально, то программа выводит число \(-i\).
Количество действий не должно превышать \(10^4\).
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
3 |
1 2 -1 3 1 |
Вы можете поиграть в эту головоломку здесь. Кликайте по дискам.
В небоскрёбе \(n\) этажей. Известно, что если уронить стеклянный шарик с этажа номер \(p\), и шарик разобьется, то если уронить шарик с этажа номер \(p+1\), то он тоже разобьется. Также известно, что при броске с последнего этажа шарик всегда разбивается.
Вы хотите определить минимальный номер этажа, при падении с которого шарик разбивается. Для проведения экспериментов у вас есть два шарика. Вы можете разбить их все, но в результате вы должны абсолютно точно определить этот номер.
Определите, какого числа бросков достаточно, чтобы заведомо решить эту задачу.
Программа получает на вход количество этажей в небоскрёбе \(n\) и выводит наименьшее число бросков, при котором можно всегда решить задачу.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
4 |
2 |
20 |
6 |
Комментарий к первому примеру. Нужно бросить шарик со 2-го этажа. Если он разобьется, то бросим второй шарик с 1-го этажа, а если не разобьется - то бросим шарик с 3-го этажа.
Подсказки.
1. Как следует действовать, если шарик был бы только один?
2. Пусть шариков два и мы бросили один шарик с этажа номер \(k\). Как мы будем действовать
в зависимости от того, разобьется ли шарик или нет?
3. Пусть f(n) - это минимальное число бросков, за которое можно определить
искомый этаж, если бы в небоскрёбе было n этажей. Выразите f(n)
через значения f(a) для меньших значений a.
Аналогично условию первой задачи, в здании \(n\ge2\) этажей, а у вас есть \(k\ge 1\) шариков. Определите минимальное количество бросков, при помощи которого можно определить минимальный номер этажа, при броске с которого шарик разбивается. При броске с этажа \(n\) шарик всегда разбивается.
Программа получает на вход два числа \(n\) и \(k\) и должна вывести одно число — необходимое число бросков.
| Ввод | Вывод |
|---|---|
4 |
2 |
20 |
6 |
Теперь в небоскрёбе \(n\) этажей, и вам нужно опять-таки определить номер минимального этажа, при броске с которого шарик разбивается, при броске с этажа \(n\) шарик всегда разбивается. Вы успеете сделать не более \(t\) бросков, \(n\le 2^t\). Определите, какое минимальное количество шариков вам нужно иметь для того, чтобы решить эту задачу не более, чем за \(t\) бросков.
| Ввод | Вывод |
|---|---|
20 |
2 |
Решите головоломку Spin Out, когда данные \(n\) дисков ориентированы вертикально, а вам нужно развернуть их горизонтально.
В этой задаче (в отличие от первой задачи) вам необходимо вывести оптимальное решение, то есть содержащее минимальное число операций.
Формат ввода-вывода в этой задаче такой же, как и в первой задаче.
Тесты к этой задаче закрытые.
На самом деле решение этой задачи практически не отличается от первой задачи, можно написать решение, которое отличается от решения первой задачи одним байтом.
| Ввод | Вывод |
|---|---|
3 |
-1 -3 1 -2 -1 |