
Напишите функцию average(a),
которая получает на вход список чисел и возвращает
среднее значение элементов данного списка.
Список содержит только числа и не пуст.
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
average([1, 7, 9]) |
5.666666666666667 |
Напишите функцию median(a, b, c),
которая получает на вход три числа и возвращает
их медиану. В решении нельзя использовать циклы.
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
median(1, 9, 7) |
7 |
Даны два действительных числа \(x\) и \(y\). Проверьте, принадлежит ли точка с координатами \((x,y)\) заштрихованному квадрату (включая его границу). На рисунке сетка проведена с шагом 1.
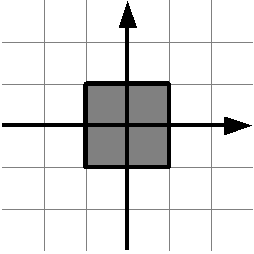
Решение оформите в виде функции is_point_in_square(x, y),
возвращающую True, если точка принадлежит квадрату и False, если не принадлежит.
Функция is_point_in_square не должна содержать инструкцию if и должна иметь
такой вид:
def is_point_in_square(x, y):
return ...
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
is_point_in_square(0, 0) |
True |
is_point_in_square(3, -7) |
False |
Решите аналогичную задачу для такого квадрата:
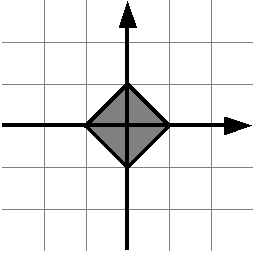
Решение должно соответствовать требованиям для решения задачи C.
Функция должна называться is_point_in_rhombus.
| Вызов функции | Возвращаемое значение |
|---|---|
is_point_in_rhombus(0, 0) |
True |
is_point_in_rhombus(1, 1) |
False |
Даны пять действительных чисел: \(x\), \(y\), \(x_c\), \(y_c\), \(r\). Проверьте, принадлежит ли точка \((x,y)\) кругу с центром \((x_c,y_c)\) и радиусом \(r\).
Решение оформите в виде функции is_point_in_circle(x, y, xc, yc, r).
Решение должно соответствовать требованиям для решения задачи C.
| Вызов функции | Возвращаемое значение |
|---|---|
is_point_in_circle(0.5, 0.5, 0, 0, 1) |
True |
is_point_in_circle(0.5, 0.5, 1, 1, 0.1) |
False |
Проверьте, принадлежит ли точка данной закрашенной области. Область неограничена снизу.
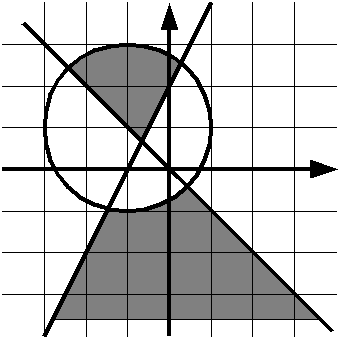
Решение оформите в виде функции is_point_in_area(x, y).
Инструкцию if использовать по-прежнему нельзя.
| Вызов функции | Возвращаемое значение |
|---|---|
is_point_in_area(-1, 2) |
True |
is_point_in_area(0, 0) |
False |
Дано число, получите число, составленное из тех же цифр, записанных в обратном порядке.
Решение оформите в виде функции reverse(n), которая получает
на вход значение типа int и возвращает значение типа int.
| Вызов функции | Возвращаемое значение |
|---|---|
reverse(179) |
971 |
Для данного числа \(n\) определите следующее за ним число, запись которого является палиндромом.
Решение оформите в виде функции next_palindrome(n), которая получает
на вход значение типа int и возвращает значение типа int.
В решении используйте функцию из предыдущей задачи. Сдайте на проверку
две функции: reverse и next_palindrome.
| Вызов функции | Возвращаемое значение |
|---|---|
next_palindrome(179) |
181 |
Дано натуральное число \(n>1\). Найдите его наименьший делитель, отличный от 1.
Решение оформите в виде функции min_divisor(n). Алгоритм должен
иметь сложность \(O(\sqrt{n})\).
Указание. Если у числа \(n\) нет делителя не превосходящего \(\sqrt{n}\), то число \(n\) — простое и ответом будет само число \(n\).
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
min_divisor(4) |
2 |
min_divisor(5) |
5 |
Дано натуральное число \(n>1\). Проверьте, является ли оно простым.
Решение оформите в виде функции is_prime(n), которая возвращает
True для простых чисел и False для составных чисел. Решение
должно иметь сложность \(O(\sqrt{n})\).
Сдайте на проверку только тело функции.
| Вызов функции | Возвращаемое значение |
|---|---|
is_prime(2) |
True |
is_prime(4) |
False |
Дано натуральное число \(n>1\).
Постройте его разложение на простые множители.
Решение должно быть оформлено в виде функции factor(n), возвращающей список
делителей числа в порядке неубывания. Каждый делитель должен быть включен в список
с учетом его кратности.
Функция должна перебирать делители до \(\sqrt{n}\), при уменьшении числа \(n\) граница перебора также должна уменьшатся.
Использование функций sqrt, pow, операции **
для извлечения квадратного корня может быть причиной долгого работы программы.
Используйте вместо них возведение в квадрат при помощи операции умножения.
| Вызов функции | Возвращаемое значение |
|---|---|
factor(132) |
[2, 2, 3, 11] |
factor(2) |
[2] |
Дано натуральное число \(n\). Посчитайте произведение его цифр, не используя строковые операции
(напишите цикл, перебирающий цифры числа). Решение оформите в виде функции product_of_digits.
| Вызов функции | Возвращаемое значение |
|---|---|
product_of_digits(179) |
63 |
В этих упражнениях необходимо реализовать функции, которые принимают в качестве параметров
два или три значения типа bool и возвращают значение типа bool. Сама функция должна содержать
только одну инструкцию return и какие-то логические операции с параметрами.
Реализуйте функцию xor(x, y), реализующую логическую операцию XOR (исключающее или, обозначается \(x \oplus y\)).
Функция возвращает True, если одно (но не оба одновременно!) из значений параметров функции
есть True. То есть функция задаётся следующей таблицей истинности (для удобства
в ней использованы числа 0 и 1 для обозначения логических величин):
| \(\ x\ \) | \(\ y\ \) | \(x\oplus y\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| Вызов функции | Возвращаемое значение |
|---|---|
xor(False, True) |
True |
Реализуйте функцию imp(x, y), реализующую логическую операцию “импликация” (следование, обозначается \(x\Rightarrow y\)).
Функция возвращает True, если из утверждения \(x\) следует утверждение \(y\),
а именно, из ложного утверждения следует как ложное, так и истинное утверждение,
а из истинного утверждения следует только истинное утверждение.
То есть функция задаётся следующей таблицей истинности.
| \(\ x\ \) | \(\ y\ \) | \(x\Rightarrow y\) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| Вызов функции | Возвращаемое значение |
|---|---|
imp(False, True) |
True |
Реализуйте функцию голосования (или большинства) major(x, y, z) (обозначается\(\langle x, y, z\rangle\)).
Функция возвращает то значение, которое встречается чаще среди её аргументов.
Функцию можно задать следующей таблицей:
| \(\ x\ \) | \(\ y\ \) | \(\ z\ \) | \(\langle x, y, z\rangle\) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| Вызов функции | Возвращаемое значение |
|---|---|
major(False, True, False) |
False |
В данных упражнениях функция выводит что-то на экран, при помощи функции print,
но не возвращает значения.
Напишите функцию histogram(a), принимающей в качестве параметра
список целых неотрицательных чисел. Функция должна напечатать на экран
столько строчек, сколько элементов в списке. \(i\)-я строка должна содержать
\(a[i]\) символов “#” (в нумерации с нуля). Функция не возвращает значения.
| Вызов функции | Вывод на экран |
|---|---|
histogram([1, 7, 9]) |
# |
Напишите функцию triangle(n), получающую в качестве параметра
целое положительное число \(n\) и выводящую на экран треугольник из \(n\) строк,
составленный из символов “*”. Первая строка содержит одну звёздочку,
каждая следующая строка содержит на 2 звёздочки больше, чем предыдущая. При этом
все строки, кроме последней, должны содержать в начале один или несколько пробелов
так, чтобы строки были выровнены по центру последней строки.
| Вызов функции | Вывод на экран |
|---|---|
triangle(4) |
* |
Напишите функцию fir(a, b), получающую на вход два целых числа
\(1\le a\le b\), и выводящую ёлочку из \(b - a + 1\) треугольников высоты
\(a\), \(a + 1\), ..., \(b\).
Используйте функцию triangle из предыдущей
задачи, модифицировав её так, чтобы она получала второй параметр: дополнительное
число пробелов, которое нужно добавить в начало каждой строки выводимого треугольника.
Самая нижняя строка ёлочки не должна содержать пробелов в начале строки.
Сдайте на проверку две функции.
По правилам оформления программ функции должны отделяться друг от друга двумя пустыми строками.
| Вызов функции | Вывод на экран |
|---|---|
fir(2, 4) |
* |
В следующих задачах функция должна считать данные с клавиатуры при помощи функции input и вернуть
что-то при помощи инструкции return.
Напишите функцию read_even(), которая
input список чисел, записанных в одной строке через пробел,
| Вызов функции | Входные данные | Возвращаемое значение |
|---|---|---|
read_even() |
1 2 3 4 5 6 |
[2, 4, 6] |
Напишите функцию read_greater(x), которая
input список чисел, записанных в одной строке через пробел,
| Вызов функции | Входные данные | Возвращаемое значение |
|---|---|---|
read_greater(2) |
1 2 3 4 5 6 |
[3, 4, 5, 6] |
read_greater(3) |
6 5 4 3 2 1 |
[6, 5, 4] |
Напишите функцию read, которая будет считывать последовательность
чисел, записанных по одному в строке, пока не встретит строку, содержащую число 0.
Числа, следующие за числом 0, считывать не нужно. Функция должна создать и вернуть список
из считанных чисел (не включая 0).
| Вызов функции | Входные данные | Возвращаемое значение |
|---|---|---|
read() |
1 |
[1, 2, 3] |
Напишите функцию read, которая будет считывать последовательность
чисел, записанных по одному в строке, пока не встретит два подряд идущих равных числа.
Функция должна вернуть это число. Последующие числа считывать не нужно.
| Вызов функции | Входные данные | Возвращаемое значение |
|---|---|---|
read() |
1 |
3 |
Напишите функцию read(k), которая будет считывать
список чисел, записанных в одной строке через пробел.
После этого функция должна вывести список тех же чисел, увеличенных на \(k\),
через пробел, и вернуть список тех же чисел, уменьшенных на \(k\).
| Вызов функции | Входные данные | Вывод на экран | Возвращаемое значение |
|---|---|---|---|
read(7) |
1 2 3 |
8 9 10 |
[-6, -5, -4] |
В этих задачах функция должна модифицировать какую-то глобальную переменную. В целом, механизм глобальных переменых не одобряется и должен использоваться только в специальных случаях.
Напишите функцию sum_list(a), которая получает в качестве параметра
список целых чисел, суммирует его элементы и добавляет их к глобальной переменной total_sum.
Сама функция не возвращает значения.
| Пример программы | Вывод на экран |
|---|---|
total_sum = 0 |
6 |
Напишите функцию max_digit(n), которая получает в качестве параметра
целое положительное число n, определяет его наибольшую цифру
и сравнивает полученное значение с глобальной переменной max_digit_value.
Если значение наибольшей цифры числа больше, чем max_digit_value,
то необходимо обновить значение max_digit_value.
Сама функция не возвращает значения.
Опять не используем работу со строками, а используем целочисленную арифметику.
| Пример программы | Вывод на экран |
|---|---|
max_digit_value = 0 |
3 |
Напишите функцию read(), которая считывает
с клавиатуры целое число и сравнивает его с предыдущим
считанным этой функцией числом. Значение предыдущего считанного числа сохраняется
в глобальной переменной prev. Если новое значение совпадает
с предыдущим считанным значением, то функция должна вернуть True,
а если не совпадает (или если это первый вызов функции), то функция должна вернуть False.
В любом случае, функция должна обновить значение переменной prev.
В этой задаче глобальная переменная prev не обязана существовать.
Для того, чтобы проверить, существует ли глобальная переменная с именем prev
можно использовать такой код:
if 'prev' in globals():
Если нужно проверить наличие переменной среди локальных переменных, то используется
словарь locals().
| Пример программы | Ввод | Вывод |
|---|---|---|
print(read()) |
8 |
False |