

Даны два целых числа A и B (при этом A≤B). Выведите все числа от A до B включительно.
| Ввод | Вывод |
|---|---|
1 |
1 2 3 4 5 |
Даны два целых числа A и В. Выведите все числа от A до B включительно, в порядке возрастания,
если A < B, или в порядке убывания в противном случае.
| Ввод | Вывод |
|---|---|
5 |
5 4 3 2 1 |
Напечатайте в порядке убывания 100 наименьших квадратов целых положительных чисел. Программа ничего не получает на вход, только выводит нужные числа.
| Ввод | Вывод |
|---|---|
10000 |
Дано натуральное число n. Напечатайте все n-значные нечетные натуральные
числа в порядке убывания.
| Ввод | Вывод |
|---|---|
1 |
9 7 5 3 1 |
По данному натуральном n вычислите сумму \(1^3+2^3+3^3+...+n^3\).
| Ввод | Вывод |
|---|---|
3 |
36 |
По данному натуральному n вычислите сумму 1×2+2×3+...+(n-1)×n.
| Ввод | Вывод |
|---|---|
4 |
20 |
2 |
2 |
По данному целому неотрицательному n вычислите значение n!
| Ввод | Вывод |
|---|---|
5 |
120 |
По данному натуральному n≥1 вычислите сумму 1+2+...+n. Ответ выведите в виде вычисленного выражение и его значения в точности, как показано в примере.
В этой задаче нельзя использовать if.
| Ввод | Вывод |
|---|---|
4 |
1+2+3+4=10 |
1 |
1=1 |
По данному натуральному n≥2 вычислите сумму 1×2+2×3+...+(n-1)×n. Ответ выведите в виде вычисленного выражение и его значения в точности, как показано в примере.
В этой задаче нельзя использовать if.
| Ввод | Вывод |
|---|---|
4 |
1*2+2*3+3*4=20 |
2 |
1*2=2 |
По данным двум натуральным числам A и B (A≤B) выведите все чётные числа на отрезке от A до B. В этой задаче нельзя использовать инструкцию if.
| Ввод | Вывод |
|---|---|
1 |
2 4 6 8 10 |
Напишите программу, которая по данному числу n от 1 до 9 выводит на экран n флагов. Изображение одного флага имеет размер 4×4 символов, между двумя соседними флагами также имеется пустой (из пробелов) столбец. Разрешается вывести пустой столбец после последнего флага и вообще допускается вывод пробелов в конце строк. Внутри каждого флага должен быть записан его номер — число от 1 до n.
Символ обратного слэша “\” в текстовых строках
имеет специальное значение. Чтобы включить в состав текстовой
строки такой символ, его нужно повторить дважды. Например,
для вывода на экран одного такого символа можно использовать
такой код: print("\\").
| Ввод | Вывод |
|---|---|
3 |
+___ +___ +___ |
1 |
+___ |
Дано 10 целых чисел. Считайте каждое из этих чисел и выведите столько символов “*” чему равно это число. Выводите число сразу же после считывания числа.
| Ввод | Вывод |
|---|---|
1 |
* |
Дано несколько чисел. Вычислите их сумму. Сначала вводите количество чисел \(N\), затем вводится ровно \(N\) целых чисел.
| Ввод | Вывод |
|---|---|
3 |
321 |
По данному натуральному числу \(n\le 1000\) выведите все натуральные делители числа \(n\) в порядке возрастания. Числа нужно выводить в одной строке через пробел (вспомните про параметры функции print).
| Ввод | Вывод |
|---|---|
10 |
1 2 5 10 |
Дано N чисел: сначала вводится число N, затем вводится ровно N целых чисел. Подсчитайте количество нулей среди введенных чисел и выведите это количество.
| Ввод | Вывод |
|---|---|
5 |
2 |
Дано 10-значное число. Выведите все цифры этого числа в обратном порядке по одной, без разделителей.
| Ввод | Вывод |
|---|---|
1234567890 |
0987654321 |
Найдите и выведите все двузначные числа, которые равны удвоенному произведению своих цифр.
Программа не требует ввода данных с клавиатуры, просто выводит список искомых чисел.
Квадрат трехзначного числа оканчивается тремя цифрами, равными этому числу. Найдите и выведите все такие числа.
Программа не требует ввода данных с клавиатуры, просто выводит список искомых чисел.
Дано натуральное число n. Выведите в порядке возрастания все трехзначные числа, сумма цифр которых равна n.
| Ввод | Вывод |
|---|---|
3 |
102 |
По данному натуральному n≤9 выведите лесенку из n ступенек, i-я ступенька состоит из чисел от 1 до i без пробелов.
| Ввод | Вывод |
|---|---|
3 |
1 |
Даны два четырёхзначных числа A и B. Выведите все четырёхзначные числа на отрезке от A до B, запись которых является палиндромом.
| Ввод | Вывод |
|---|---|
1600 |
1661 |
Даны два четырёхзначных числа A и B. Выведите в порядке возрастания все четырёхзначные числа на отрезке от A до B, запись которых содержит ровно три одинаковые цифры.
| Ввод | Вывод |
|---|---|
1900 |
1911 |
По данному натуральном \(n\) вычислите сумму \(1!+2!+3!+...+n!\). В решении этой задачи можно использовать только один цикл.
| Ввод | Вывод |
|---|---|
3 |
9 |
Рассмотрим \(N\)-домино. В таком домино каждая костяшка состоит из двух половинок, на каждой из которых нарисовано от 0 до \(N\) точек. Полный комплект костяшек такого домино содержит все возможные костяшки, каждую по одному разу. Например, для \(N=2\) в комплект войдут следующие костяшки: (0,0), (0,1), (0,2), (1,1), (1,2) и (2,2). По заданному \(N\) (\(1\le N \le 30\)) определите, сколько всего точек изображено на всех костяшках полного комплекта \(N\)-домино.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
2 |
12 |
Дана монотонная последовательность, в которой каждое натуральное число k встречается ровно k раз: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, ...
По данному натуральному n выведите первые n членов этой последовательности. Решите задачу при помощи одного цикла for. Операция умножения строки на число также не допускается.
| Ввод | Вывод |
|---|---|
2 |
1 2 |
5 |
1 2 2 3 3 |
Даны целые неотрицательные числа \(a\), \(b\), \(c\), \(d\), при этом \(a\le b\), \(0\le c \lt d\). Выведите в порядке возрастания все числа от \(a\) до \(b\), которые дают остаток \(c\) при делении на \(d\).
В этой задаче нельзя использовать инструкцию if, операторы сравнения
(< и т.д.), функции min, max, abs и т.д, должен быть только один цикл.
| Ввод | Вывод |
|---|---|
1 |
1 3 |
1 |
4 |
Необходимо заказать транспорт для перевозки \(N\) человек. Заказывать можно автобусы и такси. В каждый автобус можно посадить не более 50 человек, в каждое такси — не более 4 человек. Стоимость заказа автобуса составляет \(A\) рублей, такси — \(B\) рублей (разумеется, \(A \gt B\)).
Определите, какое количество автобусов и такси нужно заказать, чтобы потратить как можно меньшую сумму денег.
Программа получает на вход три целых числа: \(N\), \(A\), \(B\) (\(1 \le N \le 10^5\), \(1 \le B \lt A \le 1000\)).
Выведите два числа — количество автобусов и количество такси для заказа в оптимальном случае. Если возможных ответов несколько, выведите любой.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
4 |
0 1 |
Кривая дракона — один из наиболее известных фракталов. Она строится так: на первом шаге проводится отрезок из начала координатной плоскости в точку (0; 1). Далее на каждом шаге из конца фрактала повторяется уже нарисованная часть фигуры, повернутая на 90 градусов против часовой стрелки
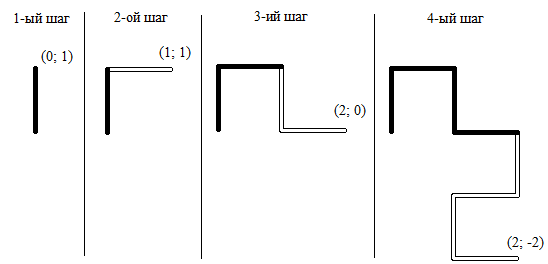
По данному числу \(N\ge 1\) определите конец кривой дракона после выполнения \(N\) шагов.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
2 |
1 1 |
4 |
2 -2 |
Магический квадрат — это таблица 3×3, в каждой из ячеек которой находятся числа от 0 до 9, числа могут повторяться, но сумма чисел в каждой строке и каждом столбце равна одному числу \(N\).
Определите по данному \(N\) сколько существует различных магических квадратов с суммой чисел в каждой строки и каждом столбце, равной \(N\).
Программа получает на вход одно целое неотрицательное число \(N\) и должна вывести искомое число вариантов.
| Ввод | Вывод |
|---|---|
0 |
1 |
1 |
6 |
Бригада скорой помощи выехала по вызову в один из отделенных районов. К сожалению, когда диспетчер получил вызов, он успел записать только адрес дома и номер квартиры \(K_1\), а затем связь прервалась. Однако он вспомнил, что по этому же адресу дома некоторое время назад скорая помощь выезжала в квартиру \(K_2\), которая расположена в подъезде \(P_2\) на этаже \(N_2\). Известно, что в доме \(M\) этажей и количество квартир на каждой лестничной площадке одинаково. Напишите программу, которая вычилсяет номер подъезда \(P_1\) и номер этажа \(N_1\) квартиры \(K_1\).
Программа получает на вход пять положительных целых чисел \(K_1\), \(M\), \(K_2\), \(P_2\), \(N_2\). Все числа не превосходят 1000.
Выведите два числа \(P_1\) и \(N_1\). Если входные данные не позволяют однозначно определить \(P_1\) или \(N_1\), вместо соответствующего числа напечатайте 0. Если входные данные противоречивы, напечатайте два числа –1 (минус один).
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
89 |
2 3 |
11 |
0 1 |
3 |
-1 -1 |
На страусиной ферме есть \(N\times M\) птиц. Каждому страусу соорудили по загону, установив перегородки так, чтобы они образовывали прямоугольник из \(N\) строк и \(M\) столбцов. Тем самым образуется ровно \(N\times M\) квадратных загонов \(1\times 1\).
В один прекрасный осенний день страус Чак, находившийся в нижнем левом загоне, почувствовал острую необходимость отправиться по важным и неотложным страусиным делам. Он начал пробивать себе путь на волю, ломая перегородки. Сначала он сломал правую перегородку и переместился загоном правее. Потом он сломал верхнюю перегородку и переместился вверх. Далее он прокладывал себе путь по такому же принципу: ломая попеременно то правую, то верхнюю перегородку, пока, наконец, не оказался на свободе.


Хозяин, увидев разгром, учиненный Чаком, сильно расстроился. Но делать нечего —надо приводить все в порядок. Он отправил письмо на ближайшую лесопилку, указав, сколько у него осталось перегородок, но забыв при этом указать, сколько ему требуется.
Помогите работникам лесопилки: зная, сколько у хозяина осталось перегородок, определите, каких размеров могла быть ферма.
Программа получает на вход одно число \(X\), \(1\le X\le 10^9\) — количество оставшихся перегородок.
Программа должна вывести все возможные варианты размеров фермы, в виде чисел \(N\) и \(M\), по одному варианту в строке. Порядок вывода вариантов не важен.
| Ввод | Вывод |
|---|---|
9 |
3 1 |