6.283185307179586
2.356194490192345
-0.7071067811865475
0.7071067811865476
Дана окружность радиуса 1, движение начинается в точке (1, 0), Вася проезжает 3/8 окружности.
В этом листочке речь пойдет о действительных числах, имеющих тип float.
Обратите внимание, что если вы хотите считать с клавиатуры действительное
число, то результат, возращаемый функцией input() необходимо
преобразовывать к типу float:
x = float(input())
Действительные (вещественные) числа представляются в виде чисел с десятичной точкой (а не запятой, как принято при записи десятичных дробей в русский текстах). Для записи очень больших или очень маленьких по модулю чисел используется так называемая запись “с плавающей точкой” (также называемая “научная” запись). В этом случае число представляется в виде некоторой десятичной дроби, называемой мантиссой, умноженной на целочисленную степень десяти (порядок). Например, расстояние от Земли до Солнца равно 1.496·1011, а масса молекулы воды 2.99·10-23.
Числа с плавающей точкой в программах на языке Питон, а также при вводе и выводе записавыются
в виде мантиссы, затем пишется буква e, затем пишется порядок. Пробелы внутри этой
записи не ставятся. Например, указанные выше константы можно записать в виде
1.496e11 и 2.99e-23. Перед самим числом также может стоять знак минус.
Напомним, что результатом операции деления / всегда является действительное число,
в то время как результатом операции // является целое число.
Преобразование действительных чисел к целому производится с округлением
в сторону нуля, то есть int(1.7) == 1, int(-1.7) == -1.
Для проведения вычислений с действительными числами язык Питон содержит много
дополнительных функций, собранных в библиотеку (модуль), которая называется math.
Для использования этих функций в начале программы необходимо подключить математическую библиотеку, что делается командой
import math
Функция от одного аргумента вызывается, например, так: math.sin(x)
(то есть явно указывается, что из модуля math используется функция sin).
Вместо числа x может быть любое число, переменная или выражение.
Функция возращает значение, которое можно вывести на экран, присвоить
другой переменной или использовать в выражении:
y = math.sin(x) print(math.sin(math.pi/2))
Другой способ использовать функции из библиотеки math, при котором не нужно будет
при каждом использовании функции из модуля math указывать название
этого модуля, выглядит так:
from math import sin, cos y = sin(x) print(sin(pi/2))
Ниже приведен список основных функций модуля math. Более подробное описание
этих функций можно найти на сайте с документацией на Питон.
Некоторые из перечисленных функций (int, round, abs)
являются стандартными и не требуют подключения модуля math для использования.
| Функция | Описание |
|---|---|
| Округление | |
int(x) |
Округляет число в сторону нуля. Это стандартная функция, для ее использования не нужно подключать
модуль math. |
round(x) |
Округляет число до ближайшего целого. Если дробная часть числа равна 0.5, то число округляется до ближайшего четного числа. |
round(x, n) |
Округляет число x
до n знаков после точки. Это стандартная функция, для ее использования не нужно подключать
модуль math. |
floor(x) |
Округляет число вниз (“пол”), при этом floor(1.5) == 1, floor(-1.5) == -2 |
ceil(x) |
Округляет число вверх (“потолок”), при этом ceil(1.5) == 2, ceil(-1.5) == -1 |
trunc(x) |
Округление в сторону нуля (так же, как функция int). |
abs(x) |
Модуль (абсолютная величина). Это - стандартная функция. |
fabs(x) |
Модуль (абсолютная величина). Эта функция всегда возвращает значение типа float. |
| Корни, степени, логарифмы | |
sqrt(x) |
Квадратный корень. Использование: sqrt(x) |
pow(a, b) |
Возведение в степень, возвращает ab. Использование: pow(a,b) |
exp(x) |
Экспонента, возвращает ex. Использование: exp(x) |
log(x) |
Натуральный логарифм. При вызове в виде log(x, b) возвращает логарифм по основанию b. |
log10(x) |
Десятичный логарифм |
e |
Основание натуральных логарифмов \(e\approx2{,}71828...\). |
| Тригонометрия | sin(x) |
Синус угла, задаваемого в радианах |
cos(x) |
Косинус угла, задаваемого в радианах |
tan(x) |
Тангенс угла, задаваемого в радианах |
asin(x) |
Арксинус, возвращает значение в радианах |
acos(x) |
Арккосинус, возвращает значение в радианах |
atan(x) |
Арктангенс, возвращает значение в радианах |
atan2(y, x) |
Полярный угол (в радианах) точки с координатами (x, y). |
hypot(a, b) |
Длина гипотенузы прямоугольного треугольника с катетами a и b. |
degrees(x) |
Преобразует угол, заданный в радианах, в градусы. |
radians(x) |
Преобразует угол, заданный в градусах, в радианы. |
pi |
Константа π |
Во всех задачах этого листка нельзя использовать строковые типы данных и операции с ними.
Дано положительное действительное число X. Выведите его целую часть.
| Ввод | Вывод |
|---|---|
17.9 |
17 |
Дано положительное действительное число X. Выведите его дробную часть абсолютно точно. Исходное число содержит не более 6 знаков после десятичной точки.
| Ввод | Вывод |
|---|---|
17.9 |
0.9 |
Дано положительное действительное число X. Выведите его первую цифру после десятичной точки. При решении этой задачи нельзя пользоваться условной инструкцией и циклом.
| Ввод | Вывод |
|---|---|
1.79 |
7 |
По российский правилам числа округляются до ближайшего целого числа, а если дробная часть числа равна 0.5, то число округляется вверх.
Дано неотрицательное число x, округлите его по этим правилам.
Обратите внимание, что функция round не годится для этой задачи!
| Ввод | Вывод |
|---|---|
2.3 |
2 |
2.5 |
3 |
С начала суток прошло \(H\) часов, \(M\) минут, \(S\) секунд (\(0\le H <12\), \(0\le M < 60\), \(0\le S < 60\)). По данным целым числам \(H\), \(M\), \(S\) определите угол (в градусах), на который повернулаcь часовая стрелка с начала суток и выведите его в виде действительного числа.
При решении этой задачи нельзя пользоваться условными инструкциями и циклами.
| Ввод | Вывод |
|---|---|
1 |
31.05 |
С начала суток часовая стрелка повернулась на угол в \(\alpha\) градусов. Определите на какой угол повернулась минутная стрелка с начала последнего часа. Входные и выходные данные — действительные числа.
При решении этой задачи нельзя пользоваться условными инструкциями и циклами.
| Ввод | Вывод |
|---|---|
190 |
120.0 |
С начала суток часовая стрелка повернулась на угол в \(\alpha\) градусов. Определите сколько полных часов, минут и секунд прошло с начала суток, то есть решите задачу, обратную задаче F. Запишите ответ в три целочисленные переменные и выведите их на экран.
При решении этой задачи нельзя пользоваться условными инструкциями и циклами.
| Ввод | Вывод |
|---|---|
31.05 |
1 2 6 |
Цена товара обозначена в рублях с точностью до копеек, то есть действительным числом с двумя цифрами после десятичной точки. Запишите в две целочисленные переменные стоимость товара в виде целого числа рублей и целого числа копеек и выведите их на экран.
При решении этой задачи нельзя пользоваться условными инструкциями и циклами.
| Ввод | Вывод |
|---|---|
10.35 |
10 35 |
Даны действительные коэффициенты \(a\), \(b\), \(c\), при этом \(a\ne0\). Решите квадратное уравнение \(ax^2+bx+c=0\) и выведите все его корни. Если уравнение имеет два корня, выведите два корня в порядке возрастания, если один корень — выведите одно число, если нет корней — не выводите ничего.
| Ввод | Вывод |
|---|---|
1 |
-1.0 2.0 |
Процентная ставка по вкладу составляет P процентов годовых, которые прибавляются к сумме вклада. Вклад составляет X рублей Y копеек. Определите размер вклада через год.
Программа получает на вход целые числа P, X, Y и должна вывести два числа: величину вклада через год в рублях и копейках. Дробная часть копеек отбрасывается.
При решении этой задачи нельзя пользоваться условными инструкциями и циклами.
| Ввод | Вывод |
|---|---|
12 |
200 48 |
Процентная ставка по вкладу составляет P процентов годовых, которые прибавляются к сумме вклада через год. Вклад составляет X рублей Y копеек. Определите размер вклада через K лет.
Программа получает на вход целые числа P, X, Y, K и должна вывести два числа: величину вклада через K лет в рублях и копейках. Дробное число копеек по истечение года отбрасывается. Перерасчет суммы вклада (с отбрасыванием дробных частей копеек) происходит ежегодно.
| Ввод | Вывод |
|---|---|
12 |
315 43 |
По данному числу n вычислите сумму \(1+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{n^2}\).
| Ввод | Вывод |
|---|---|
3 |
1.3611111111111112 |
Знаете ли вы, что этот ряд сходится к \(\pi^2/6\)?
По данному целому числу n и действительному числу x вычислите сумму \( 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+...+\frac{x^n}{n!}\)
Операцией возведения в степень пользоваться нельзя. Алгоритм должен иметь сложность O(n).
| Ввод | Вывод |
|---|---|
2 |
1.105 |
10 |
1.0 |
100 |
2.7182818284590455 |
Этот ряд сходится к \(e^x\) при росте \(n\).
По данному целому числу n и действительному числу x вычислите сумму \( 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+...+(-1)^n\frac{x^{2n}}{(2n)!}\)
Операцией возведения в степень пользоваться нельзя. Алгоритм должен иметь сложность O(n).
| Ввод | Вывод |
|---|---|
2 |
0.9950041666666667 |
10 |
1.0 |
50 |
-0.9999999999964793 |
Этот ряд сходится к \(\cos x\) при росте \(n\) (углы измеряются в радианах).
Даны длины сторон треугольник (три действительных числа). Вычислите площадь треугольника.
| Ввод | Вывод |
|---|---|
3 |
6.0 |
1 |
0.4330127018922193 |
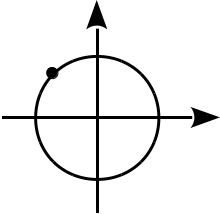
МКАД представляет собой окружность длиной \(L\). Рассмотрим систему координат, центр окружности находится в начале координат. Байкер Вася выезжает из точки пересечения МКАД с положительным направлением оси OX и едет против часовой стрелки. Определите координаты Васи после того, как он проехал расстояние \(K\).
Программа получает на вход два действительных числа \(L\) и \(K\) и должна вывести два числа — координаты Васи.
| Ввод | Вывод | Примечание |
|---|---|---|
6.283185307179586 |
-0.7071067811865475 |
Дана окружность радиуса 1, движение начинается в точке (1, 0), Вася проезжает 3/8 окружности. |
Вы находитесь в начале координат. В точке с координатами \((x, y)\) находится центр круглой колонны радиусом \(r\). Определите, под каким углом вы видите колонну.
Программа получает на вход три действительных числа \(x\), \(y\) и \(r\) и должна вывести значение угла в градусах. Гарантируется, что начало координат не находится внутри колонны.
| Ввод | Вывод | Примечание |
|---|---|---|
2 |
53.13010235415598 |
Угол немного больше 45 градусов. |
В условии предыдущей задачи вы хотите окружить колонну верёвкой, концы которой вы держите в руках. Определите минимальную длину верёвки.
Входные данные аналогичны предыдущей задаче, программа должна вывести минимальную длину верёвки.
| Ввод | Вывод |
|---|---|
2 |
8.068887871591405 |
Правильный \(n\)-угольник вписан в окружность радиуса \(r\). Найдите его периметр и площадь.
Программа получает на вход целое число \(n\ge 3\) и действительное \(r \gt 0\).
Программа должна вывести периметр и площадь данного \(n\)-угольника.
| Ввод | Вывод |
|---|---|
4 |
5.65685 |
Даны произвольные действительные коэффициенты \(a\), \(b\), \(c\). Решите уравнение \(ax^2+bx+c=0\).
Если данное уравнение не имеет корней, выведите число 0. Если уравнение имеет один корень, выведите число 1, а затем этот корень. Если уравнение имеет два корня, выведите число 2, а затем два корня в порядке возрастания. Если уравнение имеет бесконечно много корней, выведите число 3.
| Ввод | Вывод |
|---|---|
1 |
2 -1.0 2.0 |
-1 |
1 1.0 |
Дан многочлен \(P(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\) и число \(x\). Вычислите значение этого многочлена, воспользовавшись схемой Горнера: \[ P(x)= \left( ... \left( \left( \left( a_n x + a_{n-1} \right) x + a_{n-2} \right) x + a_{n-3} \right) ... \right) x + a_{0} \]
Сначала программе подается на вход целое неотрицательное число \(n\le20\), затем действительное число \(x\), затем следует \(n+1\) вещественное число — коэффициенты многочлена от старшего к младшему. Программа должна вывести значение многочлена.
При решении этой задачи нелья использовать массивы и операцию возведения в степень. Программа должна иметь сложность O(n).
| Ввод | Вывод |
|---|---|
1 |
1.0 |
2 |
1.75 |
Даны числа \(a\), \(b\), \(c\), \(d\), \(e\), \(f\). Известно, что система линейных уравнений \[ \cases{ax + by = e, \cr cx + dy = f.} \]
имеет ровно одно решение. Выведите два числа \(x\) и \(y\), являющиеся решением этой системы.
| Ввод | Вывод |
|---|---|
1 |
3.0 3.0 |
Самолет летит на высоте \(h\) метров со скоростью \(v\) м/c. Ему необходимо поразить бомбой цель. На каком расстоянии \(x\) от цели (в метрах) необходимо выпустить бомбу?
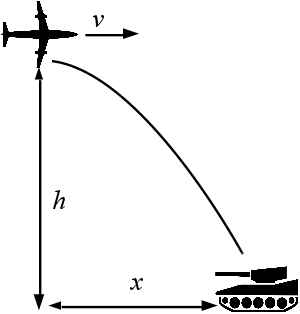
Программа получает на вход вещественные числа \(h\) и \(v\) и должна вывести значение \(x\).
В этой и последующей задачах ускорение свободного падения \(g=9.8\), сопротивлением воздуха пренебречь.
| Ввод | Вывод |
|---|---|
1000 |
4285.714285714285 |
Пушка стреляет снарядом со скоростью \(v\) м/c под углом \(\alpha\) к горизонту (в радианах). На каком расстоянии \(x\) (в метрах) от пушки упадет снаряд?
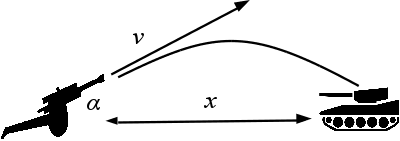
Программа получает на вход числа \(v\) и \(\alpha\) и должна вывести значение \(x\).
| Ввод | Вывод |
|---|---|
500 |
9934.141385424757 |
В условиях предыдущей задачи по данной скорости выстрела \(v\) и расстоянию до цели \(x\) определите, под каким углом \(\alpha\) к горизонту (в радианах) необходимо произвести выстрел для поражения цели.
Программа получает на вход числа \(v\) и \(x\) и должна вывести все возможные значения \(\alpha\) в порядке возрастания. Если поразить цель невозможно, программа должна вывести одно число 0.
| Ввод | Вывод |
|---|---|
500 |
0.2014022918218565 |
100 |
0 |
Пушка стреляет снарядом со скоростью \(v\) м/c и должна поразить цель, находящуюся на расстоянии \(x\) метров по горизонтали и на высоте \(y\) метров. Под каким углом \(\alpha\) к горизонту (в радианах) необходимо произвести выстрел?
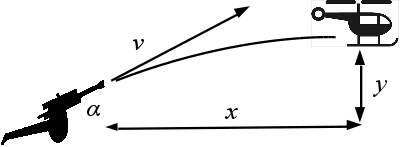
Программа получает на вход числа \(v\), \(x\), \(y\) и должна вывести все возможные значения \(\alpha\) в порядке возрастания. Если поразить цель невозможно, программа должна вывести одно число 0.
| Ввод | Вывод |
|---|---|
500 |
0.2118388917004956 |
400 |
0 |
Даны числа \(a\), \(b\), \(c\), \(d\), \(e\), \(f\). Решите систему линейных уравнений \[ \cases{ax + by = e, \cr cx + dy = f.} \]
Вывод программы зависит от вида решения этой системы.
Если система не имеет решений, то программа должна вывести единственное число 0.
Если система имеет бесконечно много решений, каждое из которых имеет вид \(y=kx+b\), то
программа должна вывести число 1, а затем значения \(k\) и \(b\).
Если система имеет единственное решение \((x_0,y_0)\), то программа должна вывести
число 2, а затем значения \(x_0\) и \(y_0\).
Если система имеет бесконечно много решений вида \(x=x_0\), \(y\) — любое, то
программа должна вывести число 3, а затем значение \(x_0\).
Если система имеет бесконечно много решений вида \(y=y_0\), \(x\) — любое, то
программа должна вывести число 4, а затем значение \(y_0\).
Если любая пара чисел \((x,y)\) является решением, то программа должна вывести число 5.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
1 |
2 3.0 3.0 |
1 |
1 -1.0 1.0 |
0 |
4 0.5 |