Даны шесть чисел: координаты центра окружности, ее радиус (в первой строке), коэффициенты нормального уравнения прямой (во второй строке).
Выведите единственное число: расстояние от данной окружности до данной прямой.
| Ввод | Вывод |
|---|---|
0 0 1 |
1.0 |
Даны шесть чисел: координаты центра окружности, ее радиус (в первой строке), коэффициенты нормального уравнения прямой (во второй строке).
В первой строке одно число K, равное количеству точек пересечения прямой с окружностью. Далее в K строках координаты самих точек.
| Ввод | Вывод |
|---|---|
1 1 1 |
2 |
Даны пять чисел: координаты центра окружности, ее радиус (в первой строке), координаты точки (два действительных числа), лежащей вне окружности (во второй строке).
Выведите единственное число: угол (в радианах), под которым видна данная окружность из данной точки.
| Ввод | Вывод |
|---|---|
1 1 1 |
1.5707963267948966 |
Даны три числа: координаты точки и угол (в радианах, задан в виде действительного числа).
Выведите координаты точки, полученной поворотом данной точки вокруг начала координат на данный угол в положительном направлении.
| Ввод | Вывод |
|---|---|
1 0 |
0.0 1.0 |
Даны четыре числа: коээфициенты нормального уравнения прямой и угол (в радианах, задан в виде действительного числа).
Выведите три числа: коэффициенты нормального уравнения прямой, полученной поворотом данной прямой вокруг начала координат на данный угол в положительном направлении.
| Ввод | Вывод |
|---|---|
1 1 -1 |
1.0 -1.0 1.0 |
Даны пять чисел: координаты центра окружности, ее радиус (в первой строке), координаты точки (во второй строке).
Выведите одно число K, равное количеству точек пересечения всевозможных касательных к окружности, проходящих через данную точку. Далее в K строках координаты самих точек пересечения касательных с окружностью.
| Ввод | Вывод |
|---|---|
1 1 1 |
2 |
Даны семь чисел – координаты центра и радиус окружности (в первой строке) и действительные координаты двух точек на ней (во второй и третьей строке), с точностью до пятого знака после запятой.
Выведите одно число: длину меньшей из дуг окружности, заключенной между указанными точками.
| Ввод | Вывод |
|---|---|
1 1 1 |
1.5707963267948966 |
Даны шесть чисел – координаты центров и радиусы двух окружностей окружности.
В случае если количество общих точек окружностей конечно, в первой строке вывести одно число K, равное этому количеству, далее в K строках координаты самих точек. Если указанных точек бесконечно много, вывести единственное число "3".
| Ввод | Вывод |
|---|---|
2 3 1 |
2 |
Пятачок и Винни-Пух каждое утро ходят пить чай в гости к Кролику. Естественно, самым коротким путем.
К сожалению, однажды Винни-Пуху пришла в голову идея вырыть ловушку для Слонопотама. Самое обидное, что они с Пятачком ее даже вырыли. Поэтому теперь каждое утро, идя в гости к Кролику, они боятся в нее провалиться.
Напишите программу, которая посчитает длину самого короткого безопасного пути от домика Винни-Пуха до домика Кролика.
Ловушка для Слонопотама представляет собой яму абсолютно круглой формы. Путь является безопасным, если он не проходит по ловушке (но может проходить по ее границе).
В первой строке входных данных записаны координаты домика Винни-Пуха \(X_B\), \(Y_В\), во второй строке — координаты домика Кролика \(X_K\), \(Y_K\), в третьей строке — координаты центра и радиус ловушки \(X_L\), \(Y_L\), \(R_L\). Все координаты — целые числа из диапазона от –32000 до 32000. Радиус ловушки — натуральное число, не превышающее 32000.
Домики Винни-Пуха и Кролика не могут находиться внутри ловушки, но могут находиться на ее границе.
Выведите в выходной файл одно число — длину самого короткого безопасного пути от домика Винни-Пуха до домика Кролика с тремя знаками после точки.
| Ввод | Вывод |
|---|---|
0 0 |
1.000 |
5 0 |
7.854 |
-5 0 |
11.861 |
Винни Пух и Пятачок отправились воровать мед у пчел, и, в очередной раз влипли в неприятности. Пятачку опять потребовалось выстрелить из своего охотничьего ружья и пробить воздушный шарик, на котором Винни Пух поднялся к дуплу за медом. При этом желательно попасть именно в шарик, не задев медведя. Вычислите оптимальную позицию для стрельбы.
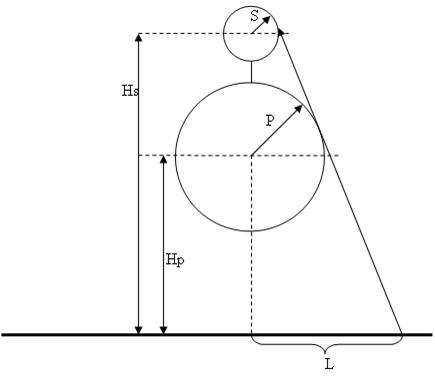
Поскольку Винни Пух очень любит покушать, то в данной задаче (да и не только в задаче) примем его за сферу радиуса \(P\). Центр медведя находится на высоте \(H_p\) над уровнем земли. Строго над медведем , находится еще одна сфера, радиуса \(S\) — воздушный шарик; центр шарика находится на высоте \(H_s\) над уровнем земли. Центры обеих сфер находятся на одной вертикальной прямой. По понятным причинам гарантируется, что сферы не пересекаются, однако могут касаться.

Считая, что ружье стреляет строго по прямой, вычислите минимальное расстояние \(L\), на которое Пятачок должен отойти от места взлета, чтобы успешно поразить шарик. Шарик считается пораженным, если траектория пули хотя бы касается его поверхности; при этом если траектория пули касается медведя, то он считается невредимым.
Вводятся положительные целые числа \(P\), \(H_p\), \(S\) и \(H_s\), не превосходящие 10000.
Выведите минимальное расстояние от точки взлета, с которого можно поразить шарик из ружья.
| Ввод | Вывод |
|---|---|
1 9 10 21 |
0.0 |