В предыдущем задании мы использовали Питон для простых разовых вычислений, используя интерактивный режим. Например, было задание вычислить длину гипотенузы прямоугольного треугольника по ее катетам. Запустите текстовый редактор и напишите следующий текст:
a = 179 b = 197 c = (a ** 2 + b ** 2) ** 0.5 print (c)
Здесь мы используем переменные — объекты, в которых можно сохранять
различные (числовые, строковые и прочие) значения. В первой строке переменной a
присваивается значение 179, затем переменной b присваивается значение 971, затем
переменной c присваивается значение арифметического выражения, равному длине гипотенузы.
После этого значение переменной c выводится на экран.
Сохраните этот текст в файле с именем hypot.py. Запустите терминал,
перейдите в каталог, где лежит этот файл и выполните эту программу:
$ python3 hypot.py
Интерпретатор языка Питон, запущенный с указанием имени файла, запускается
не в интерактивном режиме, а выполняет ту последовательность команд, которая сохранена
в файле. При этом значения вычисленных выражений не выводятся на экран (в отличии
от интерактивного режима), поэтому для того, чтобы вывести результат работы программы,
то есть значение переменной c, нам понадобится специальная функция
print.
input()Пример выше неудобен тем, что исходные данные для программы заданы в тексте программы,
и для того, чтобы использовать программу для другого треугольника необходимо исправлять
текст программы. Это неудобно, лучше, чтобы текст программы не менялся, а программа
запрашивала бы у пользователя данные, необходимые для решения задачи, то есть
запрашивала бы значения двух исходных переменных a и b.
Для этого будем использовать функцию input(), которая считывает
строку с клавиатуры и возвращает значение считанной строки, которое сразу же присвоим переменым
a и b:
a = input() b = input()
Правда, функция input возвращает текстовую строку, а нам нужно сделать так, чтобы
переменные имели целочисленные значения. Поэтому сразу же после считывания выполним преобразование
типов при помощи фунцкии int, и запишем новые значения в переменные a
и b.
a = int(a) b = int(b)
Можно объединить считывание строк и преобразование типов, если вызывать функцию int
для того значения, которое вернет функция input:
a = int(input()) b = int(input())
Далее в программе вычислим значение переменной c и выведем результат на экран.
Теперь мы можем не меняя исходного кода программы многократно использовать ее для решения
различных задач. Для того нужно запустить программу и после запуска программы ввести с клавиатуры
два числа, нажимая после кажого числа клавишу Enter. Затем программа сама выведет результат.
Дано два числа a и b. Выведите гипотенузу треугольника с заданными катетами.
| Ввод | Вывод |
|---|---|
3 |
5.0 |
print()Функция print может выводить не только значения переменных, но и значения любых выражений.
Например, допустима запись print(2 + 2 ** 2). Также при помощи функции print
можно выводить значение не одного, а нескольких выражений, для этого нужно перечислить их через запятую:
a = 1 b = 2 print(a, '+', b, '=', a + b)В данном случае будет напечатан текст
1 + 2 = 3: сначала выводится
зание переменной a, затем строка из знака “+”, затем значение переменной
b, затем строка из знака “=”, наконец, значение суммы a + b.
Обратите внимание, выводимые значение разделяются одним пробелом. Но такое поведение
можно изменить: можно разделять выводимые значения двумя пробелами, любым другим символом,
любой другой строкой, выводить их в отдельных строках или не разделять никак. Для этого
нужно функции print передать специальный именованный параметр, называемый
sep, равный строке, используемый в качестве разделителя (sep —
аббревиатура от слова separator, т.е. разделитель). По умолчанию параметр sep
равен строке из одного пробела и между значениями выводится пробел. Чтобы использовать в
качестве разделителя, например, символ двоеточия нужно передать параметр sep,
равный строке ':':
print(a, b, c, sep = ':')
Аналогично, для того, чтобы совсем убрать разделитель при выводе нужно передать параметр
sep, равный пустой строке:
print(a, '+', b, '=', a + b, sep = '')
Для того, чтобы значения выводились с новой строке, нужно в качестве параметра sep
передать строку, состоящую из специального символа новой строки, которая задается так:
print(a, b, sep = '\n')
Символ обратного слэша в текстовых строках является указанием на обозначение специального символа, в зависимости
от того, какой символ записан после него. Наиболее часто употребляется символ новой строки '\n'.
А для того, чтобы вставить в строку сам символ обратного слэша, нужно повторить его два раза: '\\'.
Вторым полезным именованным параметром функции print является параметр end,
который указывает на то, что выводится после вывода всех значений, перечисленных в функции print.
По умолчанию параметр end равен '\n', то есть следующий вывод будет происходить
с новой строки. Этот параметр также можно исправить, например, для того, чтобы убрать все дополнительные
выводимые символы можно вызывать функцию print так:
print(a, b, c, sep = '', end = '')
Напишите программу, которая считывает целое число и выводит текст, аналогичный приведенному в примере (пробелы важны!):
| Ввод | Вывод |
|---|---|
179 |
The next number for the number 179 is 180. |
Для целых чисел определены ранее рассматривавшиеся операции
+, -, * и **. Операция
деления / для целых чисел возвращает значение типа float.
Также функция возведения в степень возвращает значение типа float,
если показатель степени — отрицательное число.
Но есть и специальная операция целочисленного деления, выполняющегося с отбрасыванием
дробной части, которая обозначается //. Она возвращает целое число: целую
часть частного. Например:
>>> 17 // 3 5 >>> -17 // 3 -6
Другая близкая ей операция: это операция взятия остатка от деления, обозначаемая
%:
>>> 17 % 3 2 >>> -17 % 3 1
\(n\) школьников делят \(k\) яблок поровну, неделяющийся остаток остается в корзинке. Сколько яблок достанется каждому школьнику? Сколько яблок останется в корзинке? Программа получает на вход числа \(n\) и \(k\) и должна вывести два числа: количество яблок у каждого школьника и количество яблок, оставшихся в корзинке.
| Ввод | Вывод |
|---|---|
3 |
4 2 |
Длина Московской кольцевой автомобильной дороги —109 километров. Байкер Вася стартует с нулевого километра МКАД и едет со скоростью \(v\) километров в час. На какой отметке он остановится через \(t\) часов?
Программа получает на вход значение \(v\) и \(t\). Если \(v>0\), то Вася движется в положительном направлении по МКАД, если же значение \(v<0\), то в отрицательном.
Программа должна вывести целое число от 0 до 108 — номер отметки, на которой остановится Вася.
| Ввод | Вывод |
|---|---|
60 |
11 |
-1 |
108 |
Дано натуральное число. Выведите его последнюю цифру.
| Ввод | Вывод |
|---|---|
179 |
9 |
Дано натуральное число. Найдите число десятков в его десятичной записи (то есть вторую справа цифру его десятичной записи).
| Ввод | Вывод |
|---|---|
179 |
7 |
Дано трехзначное число. Найдите сумму его цифр.
| Ввод | Вывод |
|---|---|
179 |
17 |
Дано целое число n. Выведите следующее за ним четное число.
| Ввод | Вывод |
|---|---|
7 |
8 |
8 |
10 |
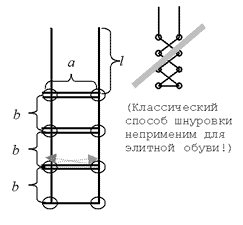
Обувная фабрика собирается начать выпуск элитной модели ботинок. Дырочки для шнуровки будут расположены в два ряда, расстояние между рядами равно \(a\), а расстояние между дырочками в ряду \(b\). Количество дырочек в каждом ряду равно \(N\). Шнуровка должна происходить элитным способом “наверх, по горизонтали в другой ряд, наверх, по горизонтали и т.д.” (см. рисунок). Кроме того, чтобы шнурки можно было завязать элитным бантиком, длина свободного конца шнурка должна быть \(l\). Какова должна быть длина шнурка для этих ботинок?

Программа получает на вход четыре натуральных числа \(a\), \(b\), \(l\) и \(N\). Программа должна выводить одно число – искомую длину шнурка.
| Ввод | Вывод |
|---|---|
2 |
26 |
В некоторой школе решили набрать три новых математических класса и оборудовать кабинеты для них новыми партами. За каждой партой может сидеть два учащихся. Известно количество учащихся в каждом из трех классов. Выведите наименьшее число парт, которое нужно приобрести для них.
Программа получает на вход три натуральных числа: количество учащихся в каждом из трех классов.
| Ввод | Вывод |
|---|---|
20 |
32 |
Дано число n. С начала суток прошло n минут. Определите, сколько часов и минут будут показывать электронные часы в этот момент. Программа должна вывести два числа: количество часов (от 0 до 23) и количество минут (от 0 до 59). Учтите, что число n может быть больше, чем количество минут в сутках.
| Ввод | Вывод |
|---|---|
150 |
2 30 |
1441 |
0 1 |
Электронные часы показывают время в формате h:mm:ss, то есть сначала записывается
количество часов, потом обязательно двузначное количество минут, затем обязательно двузначное количество секунд.
Количество минут и секунд при необходимости дополняются до двузначного числа нулями.
С начала суток прошло n секунд. Выведите, что покажут часы.
| Ввод | Вывод |
|---|---|
3602 |
1:00:02 |
129700 |
12:01:40 |
Напишите программу, которая считывает значения двух переменных a и b, затем меняет их значения местами (то есть в переменной a должно быть записано то, что раньше хранилось в b, а в переменной b записано то, что раньше хранилось в a). Затем выведите значения переменных.
| Ввод | Вывод |
|---|---|
3 |
7 3 |
Примечание. Решением задачи не является такой код:
a = input () b = input () print (b, a)
Решите предыдущую задачу без использования дополнительной переменной.
В некоторой школе занятия начинаются в 9:00. Продолжительность урока — 45 минут, после 1-го, 3-го, 5-го и т.д. уроков перемена 5 минут, а после 2-го, 4-го, 6-го и т.д. — 15 минут.
Дан номер урока (число от 1 до 10). Определите, когда заканчивается указанный урок. Выведите два целых числа: время окончания урока в часах и минутах.
| Ввод | Вывод |
|---|---|
3 |
11 35 |
2 |
10 35 |
Пирожок в столовой стоит \(a\) рублей и \(b\) копеек. Определите, сколько рублей и копеек нужно заплатить за \(n\) пирожков. Программа получает на вход три числа: \(a\), \(b\), \(n\), и должна вывести два числа: стоимость покупки в рублях и копейках.
| Ввод | Вывод |
|---|---|
10 |
20 30 |
2 |
10 0 |
Даны значения двух моментов времени, принадлежащих одним и тем же суткам: часы, минуты и секунды для каждого из моментов времени. Известно, что второй момент времени наступил не раньше первого. Определите, сколько секунд прошло между двумя моментами времени. Программа на вход получает три целых числа — часы, минуты, секунды, задающие первый момент времени и три целых числа, задающих второй момент времени. Выведите число секунд между этими моментами времени.
| Ввод | Вывод |
|---|---|
1 |
3661 |
1 |
50 |
За день машина проезжает \(n\) километров. Сколько дней нужно, чтобы проехать маршут длиной \(m\) километров?
Программа получает на вход числа \(n\) и \(m\).
| Ввод | Вывод |
|---|---|
700 |
2 |
700 |
3 |
\(n\) школьников делят \(k\) яблок “поровну”, то есть так, чтобы количество яблок, доставшихся любым двум школьникам, отличалось бы не более, чем на 1.
Программа получает на вход числа \(n\) и \(k\) и должна вывести количество школьников, которым достанется яблок меньше, чем некоторым из их товарищей.
| Ввод | Вывод |
|---|---|
7 |
5 |
7 |
0 |
Улитка ползет по вертикальному шесту высотой \(h\) метров, поднимаясь за день на \(a\) метров, а за ночь спускаясь на \(b\) метров. На какой день улитка доползет до вершины шеста?
Программа получает на вход натуральные числа \(h\), \(a\), \(b\), и должна вывести одно натуральное число. Гарантируется, что \(a>b\).
| Ввод | Вывод |
|---|---|
10 |
8 |
Дано четырехзначное число. Определите, является ли его десятичная запись симметричной. Если число симметричное, то выведите 1, иначе выведите любое другое целое число. Число может иметь меньше четырех знаков, тогда нужно считать, что его десятичная запись дополняется слева незначащими нулями.
| Ввод | Вывод |
|---|---|
2002 |
1 |
2008 |
37 |
Даны два натуральных числа n и m. Если одно из них делится на другое нацело, выведите 1, иначе выведите любое другое целое число.
| Ввод | Вывод |
|---|---|
2 |
1 |
8 |
1 |
3 |
7 |
В часах села батарейка, и они стали идти вдвое медленнее. Когда на часах было \(x_1\) часов \(y_1\) минут, правильное время было \(a_1\) часов \(b_1\) минут. Сколько времени будет на самом деле, когда часы в следующий раз покажут \(x_2\) часов \(y_2\) минут?
Программа получает на вход числа \(x_1\), \(y_1\), \(a_1\), \(b_1\), \(x_2\), \(y_2\) в указанном порядке. Все числа целые. Числа \(x_1\), \(a_1\), \(x_2\) — от 0 до 23, числа \(y_1\), \(b_1\), \(y_2\) — от 0 до 59.
Выведите два числа \(a_2\) и \(b_2\), определяющие сколько будет времени на самом деле, когда на часах будет \(x_2\) часов \(y_2\) минут.
| Ввод | Вывод |
|---|---|
12 |
10 36 |
12 |
14 0 |
Тесты к этой задаче закрытые.
В однокруговом турнире без ничьих участвовало N команд (каждая сыграла с каждой по одному матчу). Победителями считаются все команды, которые выиграли не меньше партий, чем остальные. Какое наибольшее количество победителей может быть в таком турнире?
Вводится одно натуральное число — количество команд.
Выведите одно число — наибольшее возможное количество победителей в таком турнире.
| Ввод | Вывод |
|---|---|
2 |
1 |
Тесты к этой задаче закрытые.
Напишите программу, которая считывает два целых числа \(a\) и \(b\) и выводит наибольшее значение из них. Числа — целые от 1 до 1000.
При решении задачи можно пользоваться только
целочисленными арифметическими операциями +, -,
*, //, %, =.
Нельзя пользоваться нелинейными конструкциями: ветвлениями, циклами, функциями.
| Ввод | Вывод |
|---|---|
8 |
8 |
5 |
8 |
5 |
5 |
Имеется \(N\) кг металлического сплава. Из него изготавливают заготовки массой \(K\) кг каждая. После этого из каждой заготовки вытачиваются детали массой \(M\) кг каждая (из каждой заготовки вытачивают максимально возможное количество деталей). Если от заготовок после этого что-то остается, то этот материал возвращают к началу производственного цикла и сплавляют с тем, что осталось при изготовлении заготовок. Если того сплава, который получился, достаточно для изготовления хотя бы одной заготовки, то из него снова изготавливают заготовки, из них— детали и т.д.
Напишите программу, которая вычислит, какое количество деталей может быть получено по этой технологии из имеющихся исходно \(N\) кг сплава.
Программа получает на вход три натуральных числа \(N\), \(K\), \(M\).
Выведите одно число — количество деталей, которое может получиться по такой технологии.
| Ввод | Вывод |
|---|---|
10 |
4 |
13 |
3 |
14 |
4 |
13 |
2 |
Тесты к этой задаче закрытые.