Реализация двоичного дерева поиска

В ссылочных реализациях структур данных данные хранятся в виде отдельных элементов, связанных между собой указателями. Элементы организованы либо в виде последовательности (списка), либо в виде дерева. Рассмотрим организацию ссылочной структуры данных на основе двоичного дерева поиска.

В двоичном дереве поиска хранятся элементы, которые можно сравнивать между собой при помощи операций "меньше" и "больше", например, это могут быть числа или строки.

Все элементы, которые хранятся в дереве - уникальные, то есть одно число не может быть записано в двух вершинах дерева. У каждой вершины дерева есть два поддерева - левое и правое (они могут быть и пустыми), причем в левом поддереве все элементы меньше значения, записанного в данной вершине, а в правом поддереве - больше.

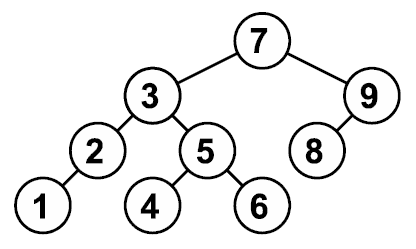
Пример правильно построенного двоичного дерева поиска:

Благодаря такому представлению, все операции с деревом (поиск элемента, добавление элемента, удаление элемента) выполняются за время, пропорциональное высоте дерева, а не его размеру. Это позволяет (используя специальные алгоритмы балансировки дерева) реализовать эффективные структуры данных типа "множество", в которых все операции осуществляются за $O(\log n)$, где $n$ -- количество элементов в множестве.

Объявление классов tree_elem и binary_tree

Для представления одной вершины (узла) двоичного дерева поиска создадим класс tree_elem. У элементов этого класса будут следующие поля:

m_data - данные (число), которые хранятся в этой вершине.

m_left - указатель на левого потомка данной вершины.

m_right - указатель на правого потомка данной вершины.

class tree_elem
{
public:
     int m_data;
     tree_elem * m_left;
     tree_elem * m_right;
     tree_elem(int val)
     {
         m_left = NULL; // В С++11 лучше использовать nullptr
         m_right = NULL;
         m_data = val;
     }
};

Конструктор для данного класса создает элемент, записывает в него переданные данные, левые и правые поддеревья инициализирует нулевыми указателями.

class binary_tree
{
private:
    tree_elem * m_root;
    int m_size;
    void print_tree(tree_elem *);
    void delete_tree(tree_elem *);

public:
    binary_tree(int);
    ~binary_tree();
    void print();
    bool find(int);
    void insert(int);
    void erase(int);
    int size();
};

m_size хранит в себе количество элементов в дереве.

Метод find() проверяет, содержится ли данный элемент в дереве, метод print() выводит все элементы поддерева, метод insert() добавляет новый элемент в дерево, метод erase() удаляет значение из дерева, метод size() возвращает значение.

Вспомогательные методы print_tree() и delete_tree() используются в рекурсивных алгоритмах обхода дерева и удаления дерева.

Конструктор

Конструктор класса binary_tree создает дерево из одного элемента. Для простоты будем считать, что в дереве всегда должен быть хотя бы один элемент.

binary_tree::binary_tree(int key)
{
m_root = new tree_elem(key);
m_size = 1;
}

Деструктор

Деструктор должен удалить все элементы дерева, для каждого из них вызвав оператор delete. Для этого реализована рекурсивная процедура delete_tree. Она рекурсивно вызывает себя для удаления левого поддерева, правого поддерева, затем удаляет сам элемент.

Сам деструктор просто вызывает рекурсивную процедуру delete_tree начиная от корня.

binary_tree::~binary_tree()
{
    delete_tree(m_root);
}

void binary_tree::delete_tree(tree_elem * curr)
{
    if (curr)
    {
        delete_tree(curr->m_left);
        delete_tree(curr->m_right);
        delete curr;
    }
}

Обход дерева

Обход дерева также реализуется рекурсивной процедурой - сначала зайдем в левое поддерево, потом в правое поддерево.

Метод print() рекурсивно обходит дерево и выводит его элементы в порядке возрастания.

void binary_tree::print()
{
    print_tree(m_root);
    cout << endl;
}

void binary_tree::print_tree(tree_elem * curr)
{
    if (curr) // Проверка на ненулевой указатель
    {
        print_tree(curr->m_left);
        cout << curr->m_data << " ";
        print_tree(curr->m_right);
    }
}

Поиск элемента в дереве

Метод find проверяет, содержится ли в дереве элемент со значением key и возвращает true или false. Поиск начинается от корня. Если key меньше того, что хранится в корне - спускаемся в левое поддерево, если больше - то в правое поддерево. Продолжаем до тех пор, пока не найдем нужный элемент, или не дойдем до пустого поддерева.

bool binary_tree::find(int key)
{
    tree_elem * curr = m_root;
    while (curr && curr->m_data != key)
    {
        if (curr->m_data > key)
            curr = curr->m_left;
        else
            curr = curr->m_right;
    }
    return curr != NULL;
}

Добавление элемента в дерево

Метод добавления элемента в дерево аналогичен методу поиска элемента - ищется позиция, где может находиться данный элемент. Если элемент не найден, то нужно создать новый элемент дерева в том месте, где он должен находиться.

void binary_tree::insert(int key)
{
    tree_elem * curr = m_root;
    while (curr && curr->m_data != key)
    {
        if (curr->m_data > key && curr->m_left == NULL)
        {
            curr->m_left = new tree_elem(key);
            ++m_size;
            return;
        }
        if (curr->m_data < key && curr->m_right == NULL)
        {
            curr->m_right = new tree_elem(key);
            ++m_size;
            return;
        }
        if (curr->m_data > key)
            curr = curr->m_left;
        else
            curr = curr->m_right;
    }
}

Удаление элемента из дерева

Удаление элемента из дерева - наиболее сложный из методов. Сначала найдем элемент, который нужно удалить (указатель curr), указатель parent указывает на его предка.

Если у curr нет левого поддерева (условие curr->m_left == NULL), то вместо curr можно подвесить его правое поддерево целиком, то есть элемент curr удаляется, а на его место становится его правое поддерево curr->m_right.

Аналогично, если у curr нет правого поддерева, то вместо него можно подвесить целиком левое поддерево.

Самый сложный случай - если у curr есть и левое, и правое поддерево. В этом случае на место элемента curr поставим наименьший элемент, который больше него. Для этого нужно спуститься в правое поддерево элемента curr, и в этом поддереве найти наименьший элемент - для этого будем двигаться указателем всегда в левого потомка текущего элемента, пока не найдем элемент, у которого нет левого потомка. Этот элемент можно удалить той же самой процедурой (т.к. у него нет левого потомка, то это простой случай удаления), а его значение записать на место элемента curr.

void binary_tree::erase(int key)
{
    tree_elem * curr = m_root;
    tree_elem * parent = NULL;
    while (curr && curr->m_data != key)
    {
        parent = curr;
        if (curr->m_data > key)
        {
            curr = curr->m_left;
        }
        else
        {
            curr = curr->m_right;
        }
    }
    if (!curr)
        return;
    if (curr->m_left == NULL)
    {
        // Вместо curr подвешивается его правое поддерево
        if (parent && parent->m_left == curr)
            parent->m_left = curr->m_right;
        if (parent && parent->m_right == curr)
            parent->m_right = curr->m_right;
        --m_size;
        delete curr;
        return;
    }
    if (curr->m_right == NULL)
    {
        // Вместо curr подвешивается его левое поддерево
        if (parent && parent->m_left == curr)
            parent->m_left = curr->m_left;
        if (parent && parent->m_right == curr)
            parent->m_right = curr->m_left;
        --m_size;
        delete curr;
        return;
    }
    // У элемента есть два потомка, тогда на место элемента поставим
    // наименьший элемент из его правого поддерева
    tree_elem * replace = curr->m_right;
    while (replace->m_left)
        replace = replace->m_left;
    int replace_value = replace->m_data;
    erase(replace_value);
    curr->m_data = replace_value;
}