2025/26, Кружок для начинающих, Стек 2 + очередь
A: Простая очередь
Реализуйте структуру данных "очередь". Напишите программу, содержащую описание очереди и моделирующую работу очереди, реализовав все указанные здесь методы. Программа считывает последовательность команд и в зависимости от команды выполняет ту
или иную операцию. После выполнения каждой команды программа должна вывести одну строчку. Возможные команды для программы:
- push n
- Добавить в очередь число n (значение n задается после команды). Программа должна вывести ok.
- pop
- Удалить из очереди первый элемент. Программа должна вывести его значение.
- front
- Программа должна вывести значение первого элемента, не удаляя его из очереди.
- size
- Программа должна вывести количество элементов в очереди.
- clear
- Программа должна очистить очередь и вывести ok.
- exit
- Программа должна вывести bye и завершить работу.
Гарантируется, что набор входных команд удовлетворяет следующим требованиям: максимальное количество элементов в очереди в любой момент не превосходит \(100\), все команды pop и front корректны, то есть при их исполнении в очереди содержится хотя
бы один элемент.
Формат входных данных
Вводятся команды управления очередью, по одной на строке
Формат выходных данных
Требуется вывести протокол работы с очередью, по одному сообщению на строке
Примеры
| Ввод | Вывод |
|---|
push 1
front
exit |
ok
1
bye |
size
push 1
size
push 2
size
push 3
size
exit |
0
ok
1
ok
2
ok
3
bye |
B: Игра в пьяницу
В игре в пьяницу карточная колода раздается поровну двум игрокам. Далее они вскрывают по одной верхней карте, и тот, чья карта старше, забирает себе обе вскрытые карты, которые кладутся под низ его колоды. Тот, кто остается без карт – проигрывает.
Для простоты будем считать, что все карты различны по номиналу, а также, что самая младшая карта побеждает самую старшую карту ("шестерка берет туза").
Игрок, который забирает себе карты, сначала кладет под низ своей колоды карту первого игрока, затем карту второго игрока (то есть карта второго игрока оказывается внизу колоды).
Напишите программу, которая моделирует игру в пьяницу и определяет, кто выигрывает. В игре участвует \(10\) карт, имеющих значения от \(0\) до \(9\), большая карта побеждает меньшую, карта со значением \(0\) побеждает карту \(9\).
Формат входных данных
Программа получает на вход две строки: первая строка содержит 5 чисел, разделенных пробелами — номера карт первого игрока, вторая – аналогично 5 карт второго игрока. Карты перечислены сверху вниз, то есть каждая строка начинается с той карты, которая будет открыта первой.
Формат выходных данных
Программа должна определить, кто выигрывает при данной раздаче, и вывести слово first или second, после чего вывести количество ходов, сделанных до выигрыша. Если на протяжении \(10^{6}\) ходов игра не заканчивается, программа должна вывести слово botva.
Примеры
| Ввод | Вывод |
|---|
1 3 5 7 9
2 4 6 8 0 |
second 5 |
2 4 6 8 0
1 3 5 7 9 |
first 5 |
C: Минимум на отрезке
Рассмотрим последовательность целых чисел длины \(N\). По ней с шагом 1 двигается “окно” длины \(K\), то есть сначала в “окне” видно первые \(K\) чисел, на следующем шаге в “окне” уже будут находиться \(K\) чисел, начиная со
второго, и так далее до конца последовательности. Требуется для каждого положения “окна” определить минимум в нём.
Формат входных данных
В первой строке входных данных содержатся два числа \(N\) и \(K\) \((1 \leq N \leq 150000, 1 \leq K \leq 10000, K \leq N)\) – длины последовательности
и “окна”, соответственно. На следующей строке находятся \(N\) чисел – сама последовательность.
Формат выходных данных
Выходые данные должны содержать \(N − K + 1\) строк – минимумы для каждого положения “окна”.
Пример
| Ввод | Вывод |
|---|
7 3
1 3 2 4 5 3 1 |
1
2
2
3
1 |
D: Гоблины и шаманы
Гоблины Мглистых гор очень любях ходить к своим шаманам. Так как гоблинов много, к шаманам часто образуются очень длинные очереди. А поскольку много гоблинов в одном месте быстро образуют шумную толку, которая мешает шаманам проводить сложные медицинские
манипуляции, последние решили установить некоторые правила касательно порядка в очереди.
Обычные гоблины при посещении шаманов должны вставать в конец очереди. Привилегированные же гоблины, знающие особый пароль, встают ровно в ее середину, причем при нечетной длине очереди они встают сразу за центром.
Так как гоблины также широко известны своим непочтительным отношением ко всяческим правилам и законам, шаманы попросили вас написать программу, которая бы отслеживала порядок гоблинов в очереди.
Формат входных данных
В первой строке входных данный записано число \(N\) (\(1\le N\le 10^5\)) - количество запросов к программе. Следующие \(N\) строк содержат описание запросов в формате:
- "+ i" - гоблин с номером \(i\) (\(1\le i \le N\)) встает в конец очереди.
- "* i" - привилегированный гоблин с номером \(i\) встает в середину очереди.
- "-" - первый гоблин из очереди уходит к шаманам. Гарантируется, что на момент такого запроса очередь не пуста.
Формат выходных данных
Для каждого запроса типа "-" программа должна вывести номер гоблина, который должен зайти к шаманам.
Примеры
| Ввод | Вывод |
|---|
7
+ 1
+ 2
-
+ 3
+ 4
-
- |
1
2
3 |
10
+ 1
+ 2
* 3
-
+ 4
* 5
-
-
-
- |
1
3
2
5
4 |
E: Гистограмма
Гистограмма является многоугольником, сформированным из последовательности прямоугольников, выровненных на общей базовой линии. Прямоугольники имеют равную ширину, но могут иметь различные высоты. Например, фигура слева показывает гистограмму, которая
состоит из прямоугольников с высотами 2, 1, 4, 5, 1, 3, 3. Все прямоугольники на этом рисунке имеют ширину, равную 1.
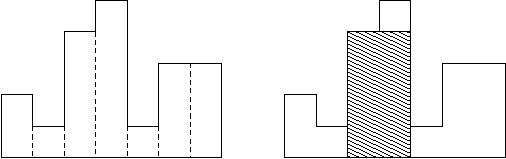
Обычно гистограммы используются для представления дискретных распределений, например, частоты символов в текстах. Отметьте, что порядок прямоугольников очень важен. Вычислите область самого большого прямоугольника в гистограмме, который также находится
на общей базовой линии. На рисунке справа заштрихованная фигура является самым большим выровненным прямоугольником на изображенной гистограмме.
Формат входных данных
В первой строке входного файла записано число \(N\) (\(0 \leq N \leq 10^{6}\)) - количество прямоугольников гистограммы. Затем следует \(N\) целых чисел \(h_1 ... h_n\), где \(0 \leq h_{i} \leq 10^{9}\). Эти числа обозначают высоты прямоугольников гистограммы
слева направо. Ширина каждого прямоугольника равна \(1\)
Формат выходных данных
Выведите площадь самого большого прямоугольника в гистограмме. Помните, что этот прямоугольник должен быть на общей базовой линии.
Примеры
| Ввод | Вывод |
|---|
7 2 1 4 5 1 3 3 |
8 |
4 1000 1000 1000 1000 |
4000 |
F: Большой, белый, очень прямоугольный
В прямоугольной таблице клетки раскрашены в белый и черный цвета. Найти в ней прямоугольную область белого цвета, состоящую из наибольшего количества ячеек.
Формат входных данных
Во входном файле записана сначала высота \(N\), а затем ширина \(M\) таблицы \((1 \le N \le 5000\), \(1 \le M \le 5000)\), а затем записано \(N\) строк по \(M\) чисел в каждой строке, где \(0\) означает, что соответствующая клетка
таблицы выкрашена в белый цвет, а \(1\) – что в черный.
Формат выходных данных
В выходной файл вывести одно число — количество клеток, содержащихся в наибольшем по площади белом прямоугольнике.
Примеры
| Ввод | Вывод |
|---|
5 6
1 0 0 0 1 0
0 0 0 0 1 0
0 0 1 0 0 0
0 0 0 0 0 0
0 0 1 0 0 0 |
9 |
4 4
0 0 0 0
0 1 0 1
0 0 0 0
1 1 0 0 |
4 |
H: Баржа
На барже располагается \(K\) грузовых отсеков. В каждый отсек можно поместить некоторое количество бочек с одним из \(10 000\) видов топлива. Причём извлечь бочку из отсека можно лишь
в случае, если все бочки, помещённые в этот отсек после неё, уже были извлечены. Таким образом в каждый момент времени в каждом непустом отсеке имеется ровно одна бочка, которую можно извлечь не трогая остальных. Будем называть такие бочки
крайними.
Изначально баржа пуста. Затем она последовательно проплывает через \(N\) доков, причём в каждом доке на баржу либо погружается бочка с некоторым видом топлива в некоторый отсек, либо выгружается крайняя бочка из
некоторого отсека. Однако, если указанный отсек пуст, либо если выгруженная бочка содержит не тот вид топлива, который ожидалось, следует зафиксировать ошибку. Если на баржу оказывается погружено более \(P\) бочек или если после прохождения всех доков она не стала пуста, следует также зафиксировать ошибку. От вас требуется либо указать максимальное количество бочек, которые одновременно пребывали на барже либо зафиксировать ошибку.
Формат входных данных
В первой строке три целых числа \(N\), \(K\) и \(P\) \((1 \le N, K, P \le 10^{5})\). Далее следует \(N\) строк с описанием действия, выполняемого в очередном доке. Если в нём происходит погрузка, то строка имеет вид «\(+\) \(A\) \(B\)», где \(A\) — номер отсека, в который помещается бочка, а \(B\) — номер вида топлива в ней. Если же док занимается разгрузкой, то строка имеет
вид «- \(A\) \(B\)», где \(A\) — номер отсека, из которого извлекается бочка, а \(B\) — номер ожидаемого вида топлива.
Формат выходных данных
Вывести либо одно число, равное искомому максимуму в случае безошибочного прохождения баржой маршрута, либо вывести слово «Error» в противном случае.
Примеры
| Ввод | Вывод |
|---|
6 1 2
+ 1 1
+ 1 2
- 1 2
- 1 1
+ 1 3
- 1 3 |
2 |
10 1 5
+ 1 1
+ 1 2
+ 1 3
+ 1 4
+ 1 5
- 1 5
- 1 4
- 1 3
- 1 2
- 1 1 |
5 |